
Motoarele moderne pentru redarea 3D, utilizate în jocuri și multimedia, sunt uimitoare în complexitatea lor în materie de matematică și programare. În consecință, rezultatul muncii lor este excelent.
Mulți dezvoltatori cred în mod eronat că crearea chiar și a celei mai simple aplicații 3D de la zero necesită cunoștințe și eforturi supraumane. Din fericire, acest lucru nu este în întregime adevărat. Mai mult decât atât, dacă aveți un computer și timp liber, puteți să vă creați ceva similar. Să aruncăm o privire asupra procesului de dezvoltare a propriului nostru motor pentru redarea 3D.
Desigur, dacă doriți să creați o aplicație 3D excelentă cu animație lină, utilizați mai bine OpenGL / WebGL. Cu toate acestea, având o idee de bază despre cum funcționează astfel de motoare, lucrul cu motoare mai complexe va părea mult mai ușor.
In acest articol voi încerca să explice de bază 3D de redare cu proiecția ortogonală, un simplu rasterizarea triunghi (procesul invers de vectorizare), Z-buffering și umbrirea plat. Nu se va concentra atenția pe lucruri, cum ar fi de optimizare, texturi și setări diferite de iluminare - dacă aveți nevoie de ea, încercați să utilizați mai potrivite pentru acest unelte scop, cum ar fi OpenGL (există o mulțime de biblioteci care vă permit să lucrați cu OpenGL, chiar folosind Java).
Exemplele de coduri vor fi în Java, însă ideile în sine pot, bineînțeles, fi aplicate în orice altă limbă la alegere.
Discuție suficientă - să trecem la afaceri!
Mai întâi, să punem ceva pe ecran. Pentru aceasta, voi folosi o aplicație simplă care afișează imaginea noastră rendered și două scroll-uri pentru rotație.
Rezultatul ar trebui să arate astfel:

Acum, să adăugăm câteva modele - noduri și triunghiuri. Vârful este doar o structură pentru stocarea celor trei coordonate (X, Y și Z), iar triunghiul conectează cele trei noduri împreună și conține culoarea lor.
Aici voi presupune că X înseamnă mișcare stânga-dreapta, Y-sus-jos, iar Z va fi adâncimea (astfel încât axa Z să fie perpendiculară pe ecran). Un Z pozitiv va însemna "mai aproape de utilizator".
De exemplu, am ales un tetraedru ca cea mai simplă figură pe care mi-am amintit - aveți nevoie de doar 4 triunghiuri pentru ao descrie.
De asemenea, codul va fi suficient de simplu - noi creăm doar 4 triunghiuri și le adăugăm în ArrayList:
Ca rezultat, obținem o figură al cărei centru este la origine (0, 0, 0), ceea ce este destul de convenabil, deoarece vom roti cifra relativă la acest punct.
Acum, să adăugăm totul pe ecran. În primul rând, nu vom adăuga capacitatea de rotație și doar tragem reprezentarea fâșiei de sârmă a figurii. Din moment ce folosim proiecția ortografică, este destul de simplu - eliminăm coordonatele Z și tragem triunghiurile noastre.
Rețineți că acum am făcut toate transformările înainte de a desena triunghiurile. Acest lucru se face astfel încât pentru a plasa centrul nostru (0, 0, 0) în centrul ecranului - în mod implicit originea se află în colțul din stânga sus al ecranului. După compilare, ar trebui să obțineți:

S-ar putea să nu credeți, dar acesta este tetraedrul nostru în proiecția ortogonală, sincer!
Acum trebuie să adăugăm rotația. Pentru a face acest lucru, trebuie să mă mut puțin de subiect și să vorbesc despre folosirea matricelor și despre modul de realizare a acestora prin intermediul transformării 3D a punctelor 3D.
Există multe modalități de a manipula puncte 3D, dar cea mai flexibilă dintre ele este utilizarea multiplicării matricelor. Ideea este de a arăta punctele sub forma unui vector de mărimea 3 × 1, iar tranziția se înmulțește, de fapt, cu o matrice de 3 × 3.
Ia vectorul nostru de intrare A:
Și multiplicați-o cu așa-numita matrice de transformare T pentru a obține vectorul de ieșire B:
De exemplu, aici este ceea ce va arăta transformarea dacă vom înmulți cu 2:
Nu puteți descrie nicio transformare posibilă utilizând matrice 3 × 3 - de exemplu, dacă tranziția are loc în afara spațiului. Puteți utiliza matrice 4 × 4, înclinate în spațiu 4D, dar acest lucru nu este prezent în acest articol.
Transformările pe care le vom folosi aici sunt scalarea și rotirea.
Orice rotire în spațiul 3D poate fi exprimată în trei rotații primitive: rotirea în planul XY, rotirea în planul YZ și rotirea în planul XZ. Putem scrie matrici de transformare pentru fiecare dintre aceste rotații în felul următor:
Și aici este locul unde începe magia: în cazul în care aveți nevoie pentru a face mai întâi un punct de rotație în planul XY folosind matricea T1 de transformare, și apoi face rotația acestui punct în planul YZ, folosind T2 matricea de transformare, atunci puteți multiplica pur și simplu T1 la T2 și pentru a obține o singură matrice, care va descrie întreaga rotație:
Aceasta este o optimizare foarte utilă - în loc să numărăm în mod constant rotațiile în fiecare punct, presupunem în prealabil o matrice și apoi o folosim.
Ei bine, matematica destul de înfricoșătoare, să ne întoarcem la cod. Să creăm o clasă de servicii Matrix3, care va ocupa multiplicările matrici-matrice și vector-matrice:
Acum puteți să vă revigorați scroller-ele de rotație. Scrollerul orizontal va controla rotirea la stânga și la dreapta (XZ), iar scrollerul vertical va controla rotirea în sus și în jos (YZ).
Să creăm matricea de rotație:
Veți avea nevoie, de asemenea, să adăugați ascultători la scrollers pentru a vă asigura că imaginea este actualizată atunci când o trageți în sus sau în jos sau de la dreapta la stânga.
După cum probabil ați observat deja, întoarcerea în sus și în jos nu funcționează. Adăugați aceste linii la cod:
Până acum, am desenat numai reprezentarea scheletului figurii noastre. Acum să o umplem cu ceva. Pentru a face acest lucru, trebuie mai întâi să rasterizăm triunghiul - să îl reprezentăm sub formă de pixeli pe ecran.
Ideea este de a calcula coordonatele barycentrice pentru fiecare pixel care poate să stea în triunghiul nostru și să excludă pe cei din afara acestuia. Următorul fragment conține un algoritm. Observați cum am accesat direct pixelii imaginii.
Destul de mult cod, dar acum avem un ecran colorat pe ecran.

Dacă jucați cu demo-ul, veți observa că nu totul este perfect - de exemplu, triunghiul albastru este întotdeauna mai mare decât alții. Acest lucru se datorează faptului că ne tragem triunghiurile unul câte unul. Albastrul este ultima, deci este desenat deasupra.
Pentru a rezolva acest lucru, să luăm în considerare z-buffer-ul. Ideea este de a crea o matrice intermediară în procesul de rasterizare, care va stoca distanța până la ultimul element vizibil pe fiecare dintre pixeli. Făcând rasterizarea triunghiurilor, vom verifica dacă distanța față de pixel este mai mică decât distanța față de cea anterioară și o pictezi numai dacă este pe partea de sus a altora.
Acum este clar că tetraedrul nostru are o latură albă:

Deci avem un motor de lucru pentru redare 3D!
Dar acest lucru nu este sfârșitul. În lumea reală, percepția unei culori variază în funcție de poziția surselor de lumină - dacă doar o cantitate mică de lumină cade pe suprafață, atunci apare mai întunecată.
În grafica pe calculator, putem obține acest efect cu așa-numita "umbrire" - schimbarea culorii suprafeței în funcție de unghiul de înclinare și de distanța față de sursa de lumină.
Cea mai simplă formă de umbrire este umbrirea plată. Această metodă ia în considerare numai unghiul dintre suprafață, normal și direcția sursei de lumină. Trebuie doar să găsiți cosinusul unghiului dintre cele două vectori și să multiplicați culoarea cu valoarea rezultată. Această abordare este foarte simplă și eficientă, deci este adesea folosită pentru randarea de mare viteză, când cele mai avansate tehnologii de umbrire sunt prea ineficiente.
În primul rând, trebuie să calculam vectorul normal pentru triunghiul nostru. Dacă avem un triunghi ABC, putem calcula vectorul său normal calculând produsul vector al vectorilor AB și AC și împărțind vectorul rezultat prin lungimea sa.
Un produs vectorial este o operație binară pe două vectori care sunt definite în spațiul 3D ca acesta:
Iată o reprezentare vizuală a ceea ce face produsul nostru vectorial:
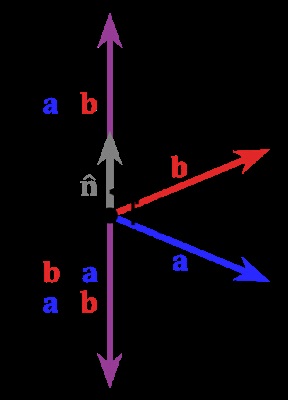
Acum trebuie să calculam cosinusul între normalul triunghiului și direcția luminii. Pentru simplificare, presupunem că sursa noastră de lumină este situată chiar în spatele camerei, la orice distanță (o astfel de configurație se numește „lumină direcțională“) - astfel, sursa noastră de lumină este la punctul (0, 0, 1).
Cosinul unghiului dintre vectori poate fi calculat prin formula:
Unde || A || Este lungimea vectorului și numitorul este produsul scalar al vectorilor A și B:
Rețineți că lungimea vectorului direcției luminii este egală cu 1, precum și lungimea normală a triunghiului (deja am normalizat acest lucru). Astfel, formula se transformă pur și simplu în acest lucru:
Observați că numai componenta Z a direcției luminii nu este egală cu zero, astfel încât să putem simplifica pur și simplu totul:
În cod, toate acestea par a fi triviale:
Omitem semnul rezultat, deoarece pentru scopurile noastre nu contează care parte a triunghiului se uită la aparatul de fotografiat. Într-o aplicație reală, va trebui să urmăriți acest lucru și să aplicați umbrirea în consecință.
Acum, după ce am obținut factorul de umbrire, putem aplica culoarea triunghiului nostru. O versiune simplă va arăta cam așa:
Codul ne va da niște efecte de umbrire, dar acestea vor scădea mult mai repede decât avem nevoie. Acest lucru se datorează faptului că Java utilizează spectrul de culori sRGB.
Așadar, trebuie să convertim fiecare culoare într-un format liniar, să aplicăm umbrirea și apoi să o convertim înapoi. Tranziția reală de la sRGB la RGB liniar este un proces destul de consumator de timp, deci nu voi efectua o listă completă de sarcini aici. În schimb, voi face ceva aproape de asta.
Și acum vedem cum animă tetraedrul nostru. Avem un motor de lucru pentru redare 3D cu culori, iluminare, umbrire, și a durat aproximativ 200 de linii de cod - nu-i rău!
Iată un mic bonus pentru dvs. - puteți crea rapid o cifră apropiată de sfera din tetraedrul dvs. Acest lucru se poate realiza prin ruperea fiecărui triunghi în 4 mici și "umflarea" acestuia.
Iată ce ar trebui să obțineți:

Aș sfârși acest articol recomandând o carte distractivă: "Bazele matematicii 3D pentru grafică și dezvoltarea jocurilor". În el, puteți găsi o explicație detaliată a procesului de redare și a matematicii în acest proces. Merită să citiți dacă sunteți interesat de motoare pentru redare.