Sistem de feedback multi-buclă.
Deschiderea unui sistem de feedback multi-buclă pentru a obține o funcție de transfer poate fi făcută într-o locație arbitrară.
Deschiderea b / a la intrarea primului link (pentru a obține funcția principală de transfer):
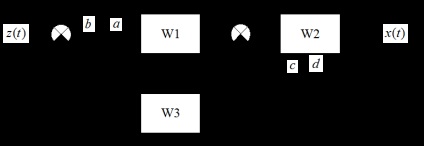
Funcția de transfer (principală):
.
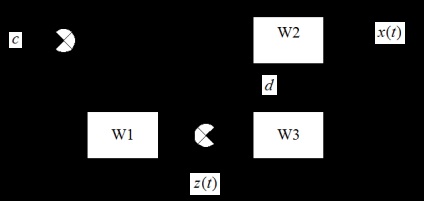
.
Funcțiile de transfer sunt diferite. Cu toate acestea, ecuațiile caracteristice ale unui sistem închis sunt aceleași:
,
.
Astfel, pentru a determina stabilitatea, putem folosi funcția de transfer a sistemului obținută prin deschiderea sistemului inițial într-un punct arbitrar. Cu toate acestea, numai funcția principală de transfer este legată de funcția de transfer a unui sistem închis prin relația binecunoscută:
.
Din faptul că în investigarea stabilității unui sistem închis suntem interesați doar de ecuația caracteristică
,
rezultă că o funcție de transfer transformată poate fi utilizată pentru a calcula stabilitatea
,
unde este un polinom arbitrar cu grad mai mic decât gradul polinomului.
.
Sisteme de control multidimensionale [1].
Sistemele multidimensionale sunt cele cu mai multe valori reglabile:
, ().
Un obiect de control multidimensional este descris de un sistem de ecuații, reprezentat de obicei într-o formă de matrice:
, , .
Aici u. f - efecte de control și deranjant (vectori).
Ecuații de mișcare în formă de matrice:
.
, ,
- matrice pătrată și dreptunghiulară a coeficienților operatorului.
Pentru imaginile Laplace (în condiții inițiale zero):
.
Aici, sunt coloane de matrice de imagini cu cantități controlate, cantități de control și perturbații.
În cazul determinantului, atunci există o matrice inversă. Înmulțind ecuația inițială din stânga prin:
- matricea funcțiilor de transfer al obiectelor pentru variabilele și tulburările de control.
Prin găsirea transformării inverse Laplace pentru fiecare element al matricilor funcțiilor de transfer ale obiectului se obține așa numita matrice Cauchy (matricea funcțiilor de greutate). De exemplu, pentru acțiunile de control
.
Dacă în momentul în care toate intrările primesc acțiuni de control, unde, atunci schimbarea celei de-a doua variabile controlate este înregistrată folosind integrala Duhamel-Carston:
.
Figura de mai jos prezintă schema bloc a unui sistem automat de control multidimensional închis. Este exact la fel ca și schema unui sistem unidimensional, doar g, x, u, y, f sunt vectori, o ,, - matrici.
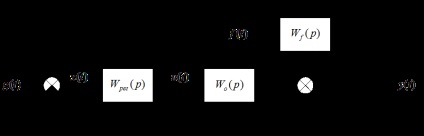
Matricea funcțiilor de transfer este deschisă pe toate canalele sistemului:
.
Matricea caracteristică a sistemului este o matrice pătrată de dimensiune, E este matricea identității:
.
Ecuația caracteristică este determinantul matricei caracteristice:
.
Matricele funcțiilor de transfer ale unui sistem închis, sistemul închis din greșeală și sistemul închis de perturbații:
, , .
Stabilitatea unui sistem bidimensional cu constrângeri antisimetrice.
Diagrama bloc a sistemului de urmărire pe două canale:
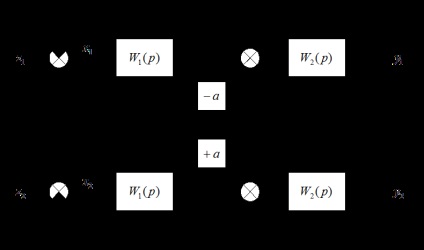
Relația valorilor de ieșire (ajustabile) cu erori:
.
.
.
.
Studiul stabilității reduce la luarea în considerare a două ecuații:
Aici, criteriul Nyquist poate fi utilizat, dar în loc de un plan complex (), care corespunde cu înregistrarea normală ecuația caracteristică, este necesar să se ia în considerare două puncte de numere complexe corespunzătoare u.
Un sistem închis va fi stabil dacă AFC a unui canal izolat în stare deschisă nu acoperă punctele și.
O limită de stabilitate oscilantă se va menține dacă una dintre egalități este satisfăcută.
Observăm că, pentru ambele puncte, contractul se încheie cu un punct, care corespunde cu formularea obișnuită a criteriului Nyquist.
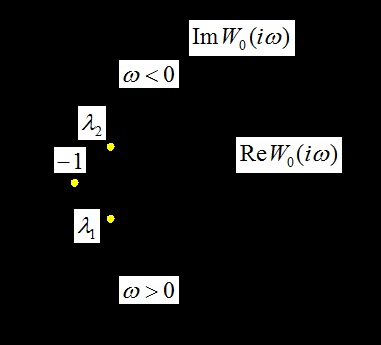
O altă metodă de calcul al stabilității unui sistem bidimensional.
Introducem ,,. Au existat rapoarte:
.
Înmulțim a doua egalitate cu i și adăugăm:
.
Aici este funcția de transfer echivalent a unui sistem bidimensional deschis, unghiul de rotație a funcției de transfer în sensul acelor de ceasornic și modulul modulului.
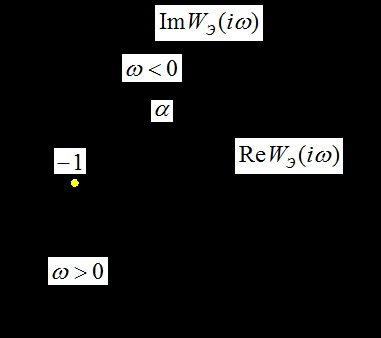
Limita de stabilitate oscilatorie, care reduce la
.
Acest lucru este în concordanță cu prima metodă de calcul al stabilității.