În unele probleme de matematică și aplicarea acesteia este impusă de valoarea cunoscută a funcțiilor trigonometrice pentru a găsi valoarea corespunzătoare a unghiului exprimat în grade sau măsură radian. Este cunoscut faptul că una și aceeași valoare a sinusului corespunde unui număr infinit de unghiuri, de exemplu, dacă $ \ păcat α = 1/2, $ unghiul $ α $ poate fi egal și $ 30 ° $ și $ 150 °, $ sau radiani $ π / 6 $ și $ 5π / 6, și $ la oricare dintre unghiurile, care se obține prin adăugarea termenului de forma $ la 360 ° ⋅k, $ sau respectiv 2πk $, $ unde $ k $ - este orice număr întreg. Acest lucru devine clar din luarea în considerare a graficului de $ y = \ sin x $ pe linia reală (a se vedea figura de $ 1 $ ..): Dacă axa $ Oy amâna $ segment de lungime 1 $ / 2 și trage o linie dreaptă paralelă cu axa de $ Ox, $ apoi trece undă sinusoidală într-un set infinit de puncte. Pentru a evita o posibilă varietate de răspunsuri introduse funcții trigonometrice inverse, altfel cunoscut sub numele de circulară sau arkfunktsiyami (de la cuvântul latin Arcus - «arc»).
Patru funcții trigonometrice de bază $ \ sin x, $ $ \ cos x, $ $ \ mathrm \, x $ și $ \ mathrm \, x $ corespund celor patru arkfunktsii $ \ arcsin x, $ $ \ ARccOS x, $ $ \ mathrm \ , x $ și $ \ mathrm \, x $ (a se citi: arcsinus, arccosinus, arctangentă, The cotangentă invers). Luați în considerare funcția \ arcsin x și \ mathrm \, x, din moment ce celelalte două sunt exprimate în termeni de următoarele formule:
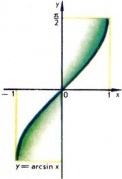
Ecuația $ y = \ arcsin mijloace x $ prin definiție un unghi $ y, $ exprimate în radiani și închise în intervalul de $ - \ frac $ la $ \ frac, $ sinus este egal cu $ x, $ adică $ \ .. . păcat y = x $ funcție $ \ arcsin x $ este o funcție a funcției inverse $ \ sin x, $ considerat pe intervalul $ \ stânga [- \ frac, + \ frac \ right], $ în cazul în care această funcție este monoton crescătoare și ia toate valoare de $ -1 $ și $ 1 + $ este clar că argumentul $ y $ funcții $ \ arcsin x $ poate lua valori doar în intervalul $ \ stânga [-1, + 1 \ dreapta]. $ Astfel, funcția $ y = \ arcsin x $ definit pe intervalul $ \ stânga [-1, + 1 \ dreapta], $ este monoton crescătoare, iar valoarea sa este umplut yayut segmentul $ \ stânga. [- \ Frac, + \ frac \ dreapta] funcția $ Program este prezentată în Fig. $ 2. $
În condiția $ -1 ≤ a ≤ 1 $, toate soluțiile ecuației $ \ sin x = a $ pot fi reprezentate ca $ x = (-1) ^ n \ arcsin a + πn, $ n = 0, ± 1, .... $ De exemplu, dacă
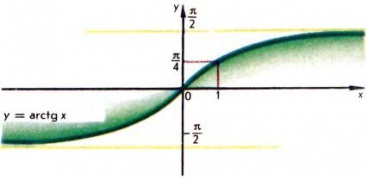
Relația $ y = \ mathrm \, x $ este definită pentru toate valorile lui $ x $ și prin definiție înseamnă că unghiul $ y, $ exprimat în măsura radianului, cuprins în