Fiecare vârf i al arborelui este asociat marcării extinse m (i). În marcarea extinsă, numărul de etichete dintr-o poziție poate fi fie un număr întreg, fie negativ, unul infinit de mare. Denumim numărul infinit de etichete prin simbolul w. ()
Vârfurile sunt clasificate în 4 tipuri:
Limitele sunt nodurile care nu au fost încă procesate de algoritm.
Algoritmul începe cu marcarea inițială. Atâta timp cât există vârfuri de graniță, ele sunt procesate de algoritm.
Fie x vârful de frontieră care trebuie procesat și cu care marcajul m (x) este legat.
1. Dacă pentru marcarea m (x) pe una din tranziții este nerezolvată, adică m (x) este un markup final, apoi x este un vertex terminal.
2. Dacă există alt vârf y în arbore. fără margini, și cu ea marcajul m (y) = m (x), atunci vârful x este un duplicat.
3. Pentru orice tranziție tj, din setul T, permis în marcajul m (x), creați un nou vertex z din arborele de accesibilitate. Marcajul m (z) asociat cu acest vârf este definit pentru fiecare poziție pi după cum urmează:
ii. dacă există un vertex y pe calea de la rădăcina arborelui la z astfel încât tj și
atunci m (z) i = w;
iii. în caz contrar
Arcul marcat cu tj este direcționat de la vârful x la vârful z. Vârful x este redefinit drept interior, iar vertexul z devine limită.
Când toate vârfurile de copaci devin terminale, redundante sau interne, algoritmul se oprește.
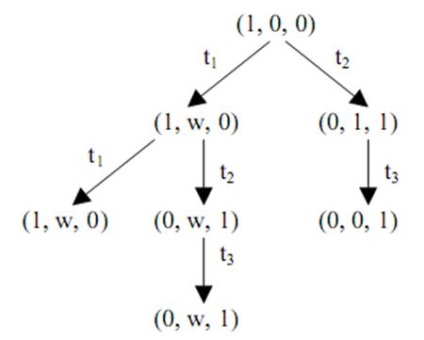
Arborele finit accesibil
Tranziția tj a rețelei Petri C se numește potențial declanșată în marcare # 956; dacă există un marcaj în R (C, # 956;); # 956; ', în care este permisă tj.
Tranziție activă în marcare # 956; dacă lansăm potențial în orice marcaj de la R (C, # 956;).
o Nivelul 0: tranziția tj nu poate fi pornită niciodată.
o Nivelul 1. Putem începe tranziția ie.
o Nivelul 2: Pentru orice număr întreg n, există o secvență de pornire în care tranziția tj este prezentă cel puțin n ori
o Nivelul 3. Există o succesiune infinită de pornire, în care tranziția tj este prezentă de nenumărate ori.
o Nivelul 4. Pentru fiecare # 956; din R (C, # 956;) există o astfel de secvență de pornire În care tranziția tj este permisă în # 948; (# 956;, # 963;).
O tranziție cu o activitate de nivel 0 se numește pasivă.
O tranziție care are o activitate de nivel 4 se numește activă.
Rețeaua Petri are nivelul de activitate i dacă fiecare dintre intersecțiile sale are nivelul de activitate i.
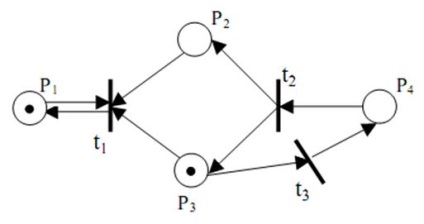
Net Petri cu tranziții de diferite nivele
t1 - primul nivel
t2 - al doilea nivel
t3 - al treilea nivel
Unele tipuri de plase Petri:
Temporal Petri net - tranzițiile au o greutate care determină durata călătoriei (întârziere).
Rețeaua stocare stochastică Petri este o variabilă aleatoare.
Rețeaua funcțională de întârziere Petri este definită ca o funcție a unor argumente, de exemplu, numărul de etichete din orice poziție, starea unor tranziții.
Etichetele de tip Petri color - etichetele pot fi de diferite tipuri, marcate cu culori, tipul de etichetă poate fi folosit ca argument în rețelele funcționale.
Rețeaua de inhibitori Petri - arce inhibitoare sunt posibile, interzicând declanșarea tranziției, dacă există o marcă în poziția de intrare asociată tranziției arcului inhibitor.
Procese de apariție și eliminare a defecțiunilor în unele sisteme tehnice, constând în multe blocuri similare. În rezervă există o unitate care poate fi utilizată; Există date statistice privind rata defecțiunilor și durata acestor operațiuni, cum ar fi depanarea, înlocuirea și repararea unității defecte. Căutarea și înlocuirea unității defecte sunt efectuate de o echipă, iar repararea unității înlocuite este efectuată de o altă echipă
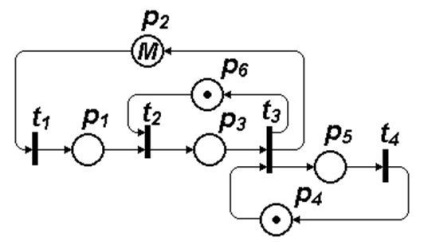
M corespunde numărului de blocuri din sistem.
t1 - blocare bloc - interval de timp între defecțiuni
t2 - căutarea unității defecte; - timpul de căutare
t3 - schimbarea unității defecte - durata înlocuirii
t4 - sfârșitul reparării - durata reparației.
Model simplificat al protocolului de schimb de date între două procese