Considerăm un sistem de ecuații lineare m cu necunoscute (1). Pentru ea
Deoarece rangul matricei este egal cu numărul său maxim liniar
rânduri independente (de teorema privind rangul matricei), atunci putem trage următoarea concluzie.
Dacă rândurile matricei extinse. și prin urmare ecuațiile sistemului (1) sunt independente liniar, atunci rangul matricei este egal cu numărul ecuațiilor sale: r = m. dacă acestea sunt dependente liniar, atunci r
Următoarele teoreme oferă răspunsuri la două întrebări importante:
1) În ce caz este sistemul (1) compatibil?
2) Dacă sistemul (1) este compatibil, câte decizii va avea el?
Teorema lui Kronecker-Capelli. Un sistem de ecuații liniare este compatibil dacă și numai dacă rangul matricei sistemului este egal cu rangul matricei extinse a acestui sistem.
Pentru un sistem comun, numărul r = r (A) = r () este numit rang al sistemului.
Teorema privind numărul de soluții. Fie rangul sistemului comun de ecuații liniare r. iar numărul de necunoscute din sistem este n. Dacă r = n. atunci sistemul are o soluție unică; dacă r
Rezultatele investigării sistemului (1) pot fi reprezentate sub forma unui circuit (figura 2).
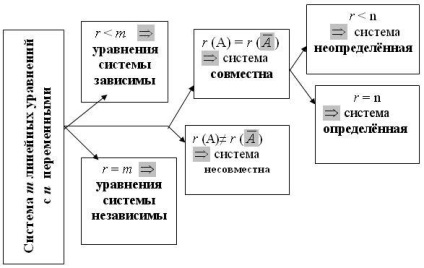
Fig. 2 Investigarea sistemelor de ecuații liniare
Să presupunem că r
Soluția sistemului (1), în care toate variabilele n-r non-basic sunt zero, se numește soluție de bază.