Orice sistem de control automat poate fi destul de complex și constă dintr-un număr de elemente, interconectate prin diferite conexiuni. Obiectul de control poate consta în conectarea mai multor obiecte, iar controlerul poate avea și alte elemente, cu excepția celor de bază considerate anterior. Apoi, diagrama structurală a sistemului de control poate avea forma
Legăturile din sistem pot fi: inverse de bază, suplimentare, suplimentare.
Conexiunea principală este formată din lanțul principal de influență (trecerea principală a sistemului). De exemplu: mob - 1 - 2 - 3 - # 966; - pentru obiect; # 966; → 4 - 5 - 6 - 7 - mreg - pentru controler.
Comunicarea suplimentară - formează o modalitate de a transfera influențe în plus față de cea principală. De exemplu: elementul 9, inclus paralel cu elementul 6.
Răspunsul suplimentar este direcționat de la ieșirea unui element la intrarea acestuia sau la intrarea elementelor anterioare. De exemplu: elementul 8 cu un semnal de la ieșirea elementului 7 la intrarea elementului 5.
Elementele incluse în sistemul de control ar trebui să fie simplu, adică să treacă semnalul de la intrare la ieșire, iar comportamentul său în timp pentru a fi descrisă printr-o ecuație diferențială nu mai mare de ordinul doi, care poate fi format considerat întotdeauna fizica procesului.
Deoarece ecuația diferențială a unui sistem complex de control este aproape imposibil de compilat, următoarea abordare este utilizată în automatizare:
1) descompun sistemul în elemente simple;
2) primesc ecuațiile diferențiale ale elementelor;
3) prin ecuațiile lor diferențiale, se obțin funcțiile lor de transfer;
4) luând în considerare conexiunile elementelor din sistemul de control, recepționează funcția de transfer a sistemului prin funcțiile de transfer ale elementelor;
5) ecuația diferențială a sistemului este obținută din funcția de transfer a sistemului.
Să facem ecuația diferențială a rezervorului cu apă ca obiect de control al nivelului apei. Acesta este un element al sistemului de reglementare (figura 13):
Fig. 13. Q1. m 3 / s - intrări de apă; Q2. m 3 / s - debitul de apă din rezervor; Secțiunea S - rezervor, = const, m2; H0 este valoarea nivelului în modul static; DH = H - H0 - abaterea nivelului de la valoarea statică (specificată); V0 - volumul lichidului din rezervor în modul static; DV - modificați volumul fluidului într-un mod dinamic.
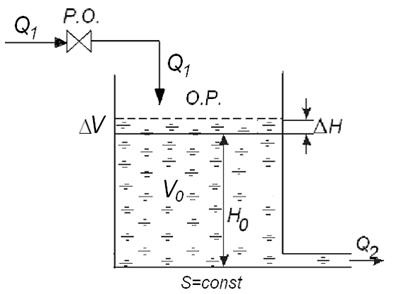
- echilibrul echilibru al cheltuielilor în dinamică
Reprezentați costurile în abateri:
(din ecuația regimului static).
Din figura rezultă că nivelul H nu afectează influxul de Q1. Nivelul H afectează debitul de apă din rezervorul Q2. în consecință, Q2 este o funcție a nivelului. În teoria sistemelor automate de control sunt luate în considerare deviații mici ale parametrului (nivelul H) de la o valoare dată (H0). În acest caz, se poate presupune că cantitățile de ieșire variază proporțional cu modificarea cantităților de intrare. Continuând de aici, se poate scrie
unde kν - coeficientul de proporționalitate (câștig).
Apoi devine ecuația dinamicii rezervorului
Se scrie ecuația (6.1) în formular
Introducem notația :; și scrieți ecuația (6.2) folosind această notație
În această ecuație, K este numit factorul de câștig dimensional. Are dimensiunea raportului dintre cantitatea de ieșire (DH) și dimensiunea cantității de intrare (DQ1). Coeficientul derivatului T [c] are dimensiunea timpului și se numește constanta de timp. Aceasta este o ecuație diferențială liniară.
În compilarea ecuația diferențială a oricăror alte sisteme de control al elementului, în care alte procese fizice au loc (de exemplu, un cuptor de încălzire), expresia de calcul R și T vor include alte mărimi fizice, dar forma ecuației poate fi aceeași.
În automatizare, cel mai adesea se ocupă de ecuații într-o formă fără dimensiuni. Atunci elementele în care există procese fizice complet diferite, dar care au același tip de ecuație diferențială, din punctul de vedere al automatizării sunt aceleași.
Forma fără formă a ecuației diferențiale a unui element.
Pentru a scrie ecuația într-o formă fără dimensiuni, alegeți valorile de bază ale cantităților care intră în ecuație. Valoarea de bază este luată ca valoarea parametrului setat (H0) și variațiile maxime posibile ale intrărilor (costurilor).
Introducem valorile fără dimensiuni ale nivelului (# 966;) și debitul de pe afluent (# 956;)
Apoi devine ecuația dinamicii rezervorului
Apoi ecuația este scrisă în forma general acceptată în teoria controlului automat
În această ecuație, T. [c] are dimensiunea timpului, prin urmare se numește constanta de timp. și k este câștigul elementului fără dimensiuni (coeficientul de transmisie).
Ecuația de statică va avea forma. din care câștigul k indică de câte ori ieșirea este mai mare sau mai mică decât valoarea de intrare în modurile de funcționare statică.
Este posibil să se formeze ecuația diferențială a a două rezervoare conectate în serie cu apă. Apoi obținem o ecuație diferențială de ordinul doi a formei
În această ecuație, coeficienții derivaților au o dimensiune de timp, deci T1 și T2 sunt constante de timp.
În elementele mai complexe, este posibil să se obțină ecuații diferențiale mai complexe, de exemplu,
Având în vedere că activitatea în viitor, cu ecuații diferențiale destul de incomode și dificile în parametrii de automatizare în funcție de timpul t, este transferat în planul numerelor complexe, prin introducerea unei varietăți de operatori. În planul acestor numere se obțin ecuații algebrice, cu care se lucrează mult mai ușor. Pentru a converti ecuații diferențiale în planul celorlalți parametri utilizați de transformata Laplace, dar este folosit mai frecvent traducerea formală a introducerii operatorului de diferențiere.
Scrieți ecuații în forma operatorului.
Utilizați ecuații diferențiale formale de transfer în formă operatorul care coincid complet cu ajutorul strict transformata Laplace, cu zero condițiile inițiale, ceea ce este practic întotdeauna făcut în teoria de control liniar.
Introducem operatorul de diferențiere:
Aici p este operatorul de diferențiere. Apoi, ecuațiile diferențiale scrise anterior în formularul operator vor avea forma:
Aceste ecuații sunt algebrice. Pentru ei se pot aplica proprietățile unei algebre, de exemplu, pentru a face un factor constant # 966; și # 956; pentru paranteze. Obținem ecuațiile de mai sus în următoarea formă.
Aceste ecuații pot fi scrise într-o formă generală:
unde D (p) se numește funcția proprie a funcției # 966; și k (p) este operatorul efectelor asupra # 956;.
Apoi, în ecuațiile de mai sus (6.12), vectorii proprii și operatorii acțiunilor sunt următorii:
Introducem noțiunea de funcție de transfer:
Definiție strictă. Funcția de transfer W (p) este raportul dintre imaginea Laplace a cantității de ieșire # P (p) la imaginea Laplace a mărimii de intrare m (p) în condiții inițiale zero
Din notarea ecuației în forma generală (6.13) rezultă că
Din (6.17), rezultă că pentru a găsi j valoarea de ieșire (p) printr-o intrare de operațiune predeterminată m (p) este suficient pentru a cunoaște W funcția de transfer (p) a elementului sau a sistemului.
A doua definiție a funcției de transfer
Prin funcția de transfer se înțelege raportul operatorului acțiunilor K (p) și funcția eigenică a funcției D (p), obținută din ecuațiile diferențiale de scriere în forma operatorului.
Cunoașterea funcțiilor de transfer ale elementelor individuale face posibilă obținerea funcțiilor de transfer ale diferitelor conexiuni de elemente și a funcției de transfer a sistemului de control.
Funcția de transfer a conexiunilor de elemente diferite.
Există trei tipuri principale de conexiuni: conexiune serială, paralelă și serială cu feedback.
1. Funcția de transfer în seria elementelor de conectare
Fig. 14. Conectarea secvențială a elementelor
Din definiția funcției de transfer rezultă că funcția de transfer a acestei conexiuni este
Din aceasta urmează
Apoi funcția de transfer a conexiunii va fi
În consecință, funcția de transfer a conexiunii în serie a elementelor este egală cu produsul funcțiilor de transfer ale tuturor elementelor.
2. Funcția de transfer a conectării paralele a elementelor.
Când elementele sunt conectate în paralel, ele au același semnal de intrare, iar semnalele de ieșire sunt însumate (Figura 15).
Prin urmare, funcția de transfer a conexiunii paralele a elementelor este egală cu suma funcțiilor de transfer ale tuturor elementelor.
Fig. 15. Conectarea paralelă a elementelor
3. Funcția de transfer a unei conexiuni seriale cu feedback.
Există conexiuni cu feedback unic și non-unitar.
Conectați-vă cu un singur feedback.
Fig. 16. Conectarea secvențială a elementelor cu un singur feedback
Funcția de transfer a feedback-ului unitar este
Feedback-urile pot fi pozitive și negative.
Pozitive - consolidează semnalul principal de intrare: xvx + xv
Negativ - slăbește semnalul principal de intrare: хвх - хвых.
Pentru a obține funcția de transfer a acestui feedback razorvom compus și efectul său asupra unui semnal deschis va lua în considerare sistemul său de administrare la intrarea primului element (x € X ± hvyh). Obținem o conexiune serială a trei elemente, a căror funcție de transfer este cunoscută - produsul funcțiilor de transfer. Prin definiție, funcția de transfer a unui sistem închis este
Funcția de transmisie cu buclă deschisă
De aici se poate obține funcția de transfer a unui sistem închis:
Semnul "-" din numitor (6.20) indică faptul că feedback-ul pozitiv este utilizat în sistem. Cu o creștere a semnalului de intrare, xv va crește, ceea ce contrazice sensul procesului de reglementare. Prin urmare, din motive de reglementare, feedback-ul pozitiv nu este adecvat. Se utilizează în principal în diferite tipuri de amplificatoare de semnal de intrare.
Semnul "+" din numitor (6.20) indică faptul că feedback-ul negativ este utilizat în sistem. Pe măsură ce semnalul de intrare crește, xv va scădea. În consecință, feedbackul negativ este utilizat în sistemele de reglementare. Apoi, funcția de transfer a sistemului va avea forma
Conectarea la un feedback non-unitar (Figura 16.)
Fig. 17. Legătura secvențială a elementelor cu feedback non-unitar
Funcția de transfer a feedback-ului prin definiție
Dacă deschideți sistemul, atunci la intrarea în elementul 1 va exista un semnal. După ce am făcut același lucru ca și pentru un singur feedback, obținem funcția de transfer a unui sistem închis cu feedback negativ în formă
Să estimăm influența feedback-ului asupra modificării cantității de ieșire a sistemului xv atunci când se modifică variabila de intrare xxx. având în vedere un sistem deschis de trei elemente (6.18) și un feedback închis al unității (6.21) și o unitate (6.22).
Fie ca elementele sistemului să fie cele mai simple, având funcții de transfer egale cu factorii de amplificare: ; ; . Apoi în sistemul deschis (Fig.14) valoarea de ieșire va fi egală cu. adică, xv cu o schimbare în xBx va varia semnificativ în K times ().
Într-un sistem închis cu un singur feedback
adică xv va varia nesemnificativ, în comparație cu schimbarea în xvx.
În sistemele închise cu feedback non-unitar ()
Schimbând influența asupra sistemului de feedback (k4) într-o gamă largă, este posibil să influențezi schimbarea cantității de ieșire xv la valori constante ale k1; k2; k3.
Să considerăm sistemul automatizat de control (ATS) ca agregat al obiectului de reglare și al regulatorului (Figura 18) prin intermediul canalului de reglare a influenței canalului
Fig. 18. Sistem de control automat
Pe baza formulelor (6.22) pentru un sistem de control închis, este posibilă notarea funcției de transfer
Deoarece obiectul de control are o funcție de transfer bine definită Wob (p), care este practic imposibil de schimbat, este posibil să se influențeze comportamentul sistemului de control numai prin schimbarea proprietăților regulatorului (schimbarea valorilor lui Vper (p)).
Funcția de transfer a unui sistem complex.
În sistemele complexe pot exista diferite legături de elemente. Pentru a determina funcția de transfer a unui sistem complex, sunt identificate regiunile cu diferiți compuși. Folosind formulele funcțiilor de transfer ale conexiunilor, ele își găsesc funcțiile de transfer și ajustează sistemul într-o formă cunoscută - o conexiune serială cu feedback.
Fig. 20. Un sistem complex de elemente de conectare
Presupunem că funcțiile de transfer W1 ... W15 sunt cunoscute. Să separăm în acest sistem compușii complexi: I, II și III.
Definiți funcțiile de transfer ale acestor compuși: WI. WII; WIII.
I - conexiune paralelă a două lanțuri de elemente: 3 - 4 și 7 - 8
II - conexiune cu feedback, care include elementul 14
III - conectarea paralelă a elementelor 12 și 15
Obținem o conexiune consecutivă a elementelor cu feedback-ul, care include.
Funcția de transfer a unui sistem complex va fi
unde este funcția de transfer a conexiunii directe a elementelor; funcția de transfer a feedback-ului.