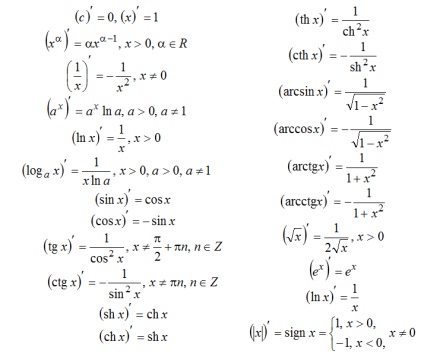Considerăm o funcție care este definită și continuă la un interval de timp al unui punct arbitrar și valoarea corespunzătoare a funcției în acest punct.Folosim argumentul funcției o incrementare în punct.De rezultat, obținem valoarea și valoarea corespunzătoare a funcției
O funcție derivată la un punct este limita raportului dintre incrementarea unei funcții și incrementarea argumentului său la acel punct, cu condiția ca aceasta să aibă tendința de zero:
Dacă această limită este finită, atunci funcția în cauză se consideră a fi diferențiată la un punct.
Diferențierea este procesul de găsire a derivatului unei funcții. Se efectuează folosind un tabel de derivate și reguli de diferențiere. Pe această pagină, toate formulele funcțiilor derivate sunt dezasamblate.
Tabel cu derivate, lista cu formula