Sarcina principală a cinematicii punctului este de a dezvolta metode de specificare a mișcării unui punct și de metode pentru determinarea caracteristicilor cinematice de bază ale mișcării.
Sarcina principală a cinematica de corp rigide este de a dezvolta metode de sarcini de mișcare și metode care permit bazate pe un număr mic de caracteristici care sunt comune pentru toate punctele pentru a găsi caracteristicile cinematice ale fiecărui punct al corpului.
Pentru a specifica mișcarea unui punct înseamnă a indica un aparat matematic cu ajutorul căruia, în orice moment dat, determină poziția unui punct în spațiu.
3. Vector, coordonate și modul natural de definire a mișcării unui punct
Pentru a specifica mișcarea unui punct înseamnă definirea unui aparat matematic, cu ajutorul căruia este posibil să se determine poziția unui punct în spațiu în orice moment dat.
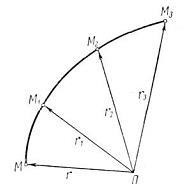
Odată cu trecerea timpului, punctul își schimbă poziția în spațiul corpului de referință. Prin urmare, vectorul de rază se schimbă atât în direcție cât și în magnitudine și este o anumită funcție vectorală a argumentului scalar t. . Dacă funcția este specificată sau cunoscută, atunci este o metodă vectorală pentru specificarea unui punct.
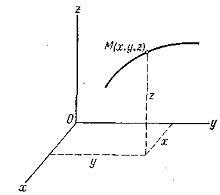
Dacă funcțiile sunt cunoscute sau specificate, atunci vorbim de metoda de coordonate de specificare a mișcării.
Să ne cunoaștem traiectoria punctului. Pe această traiectorie alegem un punct arbitrar O. Poziția punctului M pe traiectorie poate fi specificată cu ajutorul coordonatelor arcului.
Cu trecerea timpului, coordonatele arcului se schimbă și reprezintă o anumită funcție. Dacă funcția este dată, vorbim despre o modalitate firească de a specifica mișcarea unui punct.
4. Determinarea vitezei și a accelerației în modul vectorial de mișcare.
Când procesul de atribuire vectorul de mișcare a poziției punctului de mișcare la fiecare dată este determinată de vectorul rază care este o funcție de timp, atunci când se deplasează punctul de de raza este incrementat. Raportul dintre vectorul de deplasare și intervalul de timp. în care are loc această mișcare, este vectorul vitezei medii a punctului :.
Viteza vectorului unui punct la un moment dat este egală cu derivatul vectorului de rază al punctului în raport cu timpul:
Viteza vectorului punctului este tangentă la traiectoria în direcția mișcării punctului.
Să presupunem că în momentul inițial punctul are o viteză. și după un timp devine increment. Împărțirea incrementului cu intervalul de timp. obținem vectorul de accelerare medie a acestui punct în acest interval de timp. Vectorul de accelerație al unui punct este egal cu primul derivat al vitezei sau al doilea derivat al vectorului de rază al punctului în timp.
Vectorul accelerație este direcționată de-a lungul tangentei la viteza izvor de falie - locul tuturor vectorilor punctului în mișcare viteza de înregistrare de către același punct arbitrar în spațiu.
5. Determinarea vitezei și accelerației cu metoda coordonatelor de specificare a mișcării unui punct
Fie ca ecuațiile de mișcare ale unui punct să fie date:
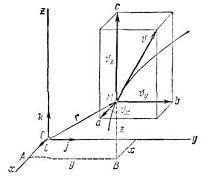
Calculând proiecția vitezei pe axele de coordonate carteziene, putem determina modulul și direcția vectorului de viteză prin următoarele formule:
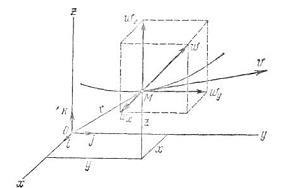
Calculând proiecția accelerației pe axele de coordonate, putem determina modulul și direcția accelerației conform următoarelor formule:
6. Determinarea vitezei și accelerației în modul natural de specificare a mișcării unui punct
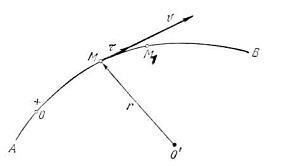
Suntem de acord să denotăm valoarea algebrică a vitezei cu ajutorul simbolului. iar modulul de viteză este o literă. apoi:
și anume modulul de viteză este egal cu valoarea absolută a derivatului coordonatelor arcului punctului în raport cu timpul.
Proiecția accelerației este egală cu punctul de tangență al doilea derivat al punctului de arc coordonatele în timp sau prima derivată din valoarea algebrică a vitezei la punctul de timp.
Miscarea progresiva a corpului. Setați mișcarea. Distribuția vitezelor și accelerațiilor punctelor corpului
Mișcarea progresivă a unui corp rigid este o mișcare în care orice linie dreaptă care leagă două puncte ale corpului se mișcă paralel cu ea însăși.
Teorema. Toate punctele unui corp rigid care se mișcă transversal descriu aceleași traiectorii (coincide cu suprapunerea) și în fiecare moment al timpului au viteze și accelerații egale geometric.
Ecuațiile de mișcare translațională a unui corp rigid sunt ecuațiile de mișcare a oricărui punct al acestui corp - de obicei ecuațiile de mișcare a centrului său de greutate:
Comună pentru toate punctele unui corp solid care se mișcă transversal, viteza de accelerare se numește viteza și accelerația mișcării translaționale a unui corp rigid.
Miscarea rotativa. Setați mișcarea
Rotația este o mișcare a corpului, în care toate punctele sale rămân fixe, situate pe o linie dreaptă numită axa de rotație.
În această mișcare, toate celelalte puncte ale corpului se mișcă în planuri perpendiculare pe axa de rotație și descriu cercuri ale căror centre se află pe această axă.
Când corpul se rotește, unghiul de rotație se schimbă în timp :.
Mărimea care caracterizează rapiditatea modificării unghiului de rotație în timp se numește viteza unghiulară a corpului.
Mărimea care caracterizează rata de schimbare a vitezei unghiulare în timp se numește accelerația unghiulară a corpului.
Ecuația de rotație uniformă a corpului. Rotația unui corp cu o viteză constantă se numește uniformă.
Ecuația de rotație uniformă a corpului. Rotația corpului, în care accelerația unghiulară este constantă, se numește rotație alternantă.