
Stare:
Corpul se rotește cu accelerație constantă accelerație unghiulară ε = 2 rad / s, este la momentul t1 = 2,5 c ω1 = viteza unghiulară de 40 rad / s.
Definiți: 1) viteza și accelerația unui punct corp situat la o distanță h = 55 cm față de axa de rotație a momentului t2 = 7 s; 2) numărul de revoluții N ale corpului pentru un timp t3 = 10 c; ecuația mișcării de rotație a corpului, dacă la momentul inițial t0 = 0, unghiul inițial de rotație φ0 = 0.
soluţie:
1. Cu rotație uniform accelerată, viteza unghiulară a corpului se modifică în conformitate cu legea
Cunoscând valoarea vitezei unghiulare co 1, la un timp t1 și unghiulare de accelerare α, poate fi găsit inițial ω0 vitezei unghiulare la t0 = 0:
Prin urmare, viteza unghiulară a corpului la momentul t2 = 7 s va fi egală cu
Viteza de Uskorenieα V și punctul M al corpului, separate de o distanță h = 55 cm față de axa de rotație, în momentul t2 = 7 va fi egal cu:
v = ω2 · h = 49,55 = 2695 cm / s = 26,95 m / s;
αvr = ε · h = 2 · 55 = 110 cm / s 2 = 1,10 m / s 2;
αo = ω 2 · h = 49 2 · 55 = 132055 cm / s 2 = 1320,6 m / s 2;
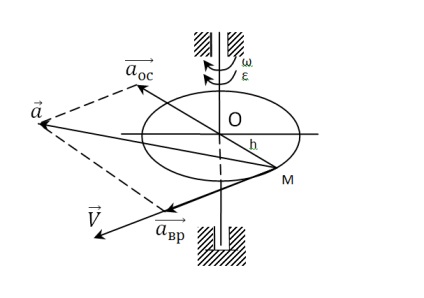
Direcția vectorilor vitezei și accelerației este prezentată în figură a sarcinii.
Numărul de rotații ale corpului într-un timp t3 = 10 c este determinat de relația
unde n (t) este numărul de revoluții ale corpului pe secundă la un moment dat.
În problema pe care o analizăm
Ecuația mișcării de rotație φ = φ (t) se obține din raportul? (T) = dφ / dt => dφ = ω (t) · dt. Integrarea acestei ecuații diferențiale cu condițiile inițiale (t0 = 0, φ0 = 0):
Se finalizează soluția problemei mecanicii teoretice în cinematică.
Cu stimă, administratorul site-ului.