principal nbsp> nbsp tutorial Wiki nbsp> nbsp Math nbsp> clasa nbsp9 nbsp> nbsp Proprietățile sinusului, cosinusului, tangentei și cotangentei
Proprietăți sinusale
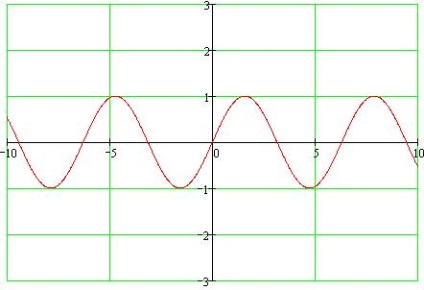
- 1. Domeniul de aplicare al definiției: întreaga axă numerică
- 2. Gama de valori: [-1; 1]
- 3. Funcția ciudată.
- 4. Cea mai mică perioadă pozitivă: 2 * pi
- 5. Coordonatele punctelor de intersecție a graficului funcției cu axa Ox: (pi * n; 0)
- 6. Coordonatele punctelor de intersecție a graficului funcției cu axa Oy: (0; 0)
- 7. Intervalele la care funcția este pozitivă: (2 * pi * n; pi + 2 * pi * n)
- 8. Intervale pe care funcția este negativă: (-pi + 2 * pi * n; 2 * pi * n)
- 9. Intervalele de creștere: [-pi / 2 + 2 * pi * n; pi / 2 + 2 * pi * n]
- 10. Intervale de scădere: [pi / 2 + 2 * pi * n; 3 * pi / 2 + 2 * pi * n]
- 11. Punctele minime: -pi / 2 + 2 * pi * n
- 12. Valoarea minimă a funcției: -1
- 13. Punctele maximului: pi / 2 + 2 * pi * n
- 14. Maximul funcției: 1
Proprietățile cosinelor
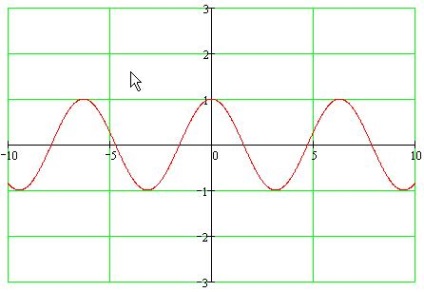
- 1. Domeniul de aplicare al definiției: întreaga axă numerică
- 2. Gama de valori: [-1; 1]
- 3. Chiar și funcția.
- 4. Cea mai mică perioadă pozitivă: 2 * pi
- 5. Coordonatele punctelor de intersecție a graficului funcției cu axa Ox: (pi / 2 + pi * n; 0)
- 6. Coordonatele punctelor de intersecție a graficului funcției cu axa Oy: (0; 1)
- 7. Intervalele la care funcția este pozitivă: (-pi / 2 + 2 * pi * n; pi / 2 + 2 * pi * n)
- 8. Intervalele la care funcția este negativă: (pi / 2 + 2 * pi * n; 3 * pi / 2 + 2 * pi * n)
- 9. Lacune de creștere: [-pi + 2 * pi * n; 2 * pi * n]
- 10. Intervale de scădere: [2 * pi * n; pi + 2 * pi * n]
- 11. Punctele minime sunt: pi + 2 * pi * n
- 12. Valoarea minimă a funcției: -1
- 13. Puncte de maxim: 2 * pi * n
- 14. Maximul funcției: 1
Proprietățile tangentei
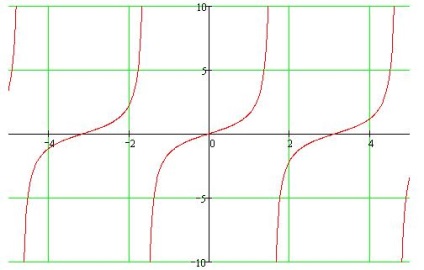
- 1. Domeniul de definiție: (-pi / 2 + pi * n; pi / 2 + pi * n)
- 2. Domeniul de aplicare al valorilor: întreaga axă numerică
- 3. Funcția ciudată.
- 4. Cea mai mică perioadă pozitivă: pi
- 5. Coordonatele punctelor de intersecție a graficului funcției cu axa Ox: (pi * n; 0)
- 6. Coordonatele punctelor de intersecție a graficului funcției cu axa Oy: (0; 0)
- 7. Intervalele la care funcția este pozitivă: (pi * n; pi / 2 + pi * n)
- 8. Intervale pe care funcția este negativă: (-pi / 2 + pi * n; pi * n)
- 9. Funcția crește pe intervale (-pi / 2 + pi * n; pi / 2 + pi * n)
- 10. Nu există puncte înalte și joase.
Proprietăți Cotangent
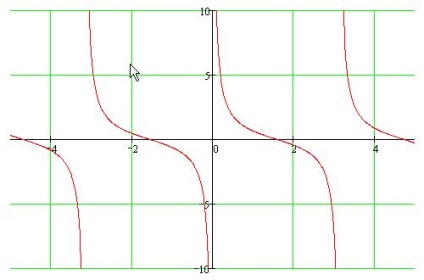
- 1. Domeniul de definiție: (pi * n; pi + pi * n)
- 2. Domeniul de aplicare al valorilor: întreaga axă numerică
- 3. Funcția ciudată.
- 4. Cea mai mică perioadă pozitivă: pi
- 5. Coordonatele punctelor de intersecție a graficului funcției cu axa Ox: (pi / 2 + pi * n; 0)
- 6. Coordonatele punctelor de intersecție ale graficului funcțional cu axa Oy: nr
- 7. Intervalele la care funcția este pozitivă: (pi * n; pi / 2 + pi * n)
- 8. Intervale pe care funcția este negativă: (-pi / 2 + pi * n; pi * n)
- 9. Funcția scade la intervale (pi * n; pi + pi * n)
- 10. Nu există puncte înalte și joase.
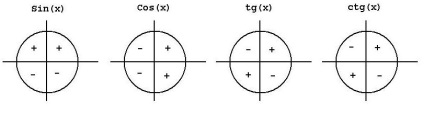
Figura de mai jos prezintă mai multe cercuri unice, în care semnele sinus, cosinus, tangente și cotangente sunt indicate în diferite sferturi de coordonate.