Forma generală a ecuației neliniare:
unde funcția f (x) este definită și continuă pe un interval finit sau infinit [a, b].
Fiecare număr care caracterizează f (x) până la zero se numește rădăcina ecuației (1). Ecuațiile neliniare sunt împărțite în ecuații algebrice și transcendente.
Ecuația (1) se consideră a fi algebrică dacă funcția f (x) este algebrică. Ecuația (1) se numește transcendent dacă funcția f (x) nu este algebrică.
Rezolvarea ecuației (1) înseamnă următoarele:
1) determinați dacă ecuația are rădăcini.
2) determina numărul rădăcinilor.
3) găsiți valorile rădăcinilor cu o anumită precizie.
Primele două etape se numesc separarea rădăcinilor. Separarea rădăcinilor este procedura de identificare a segmentelor pe care ecuația (1) are o singură rădăcină. În cele mai multe cazuri, separarea rădăcinilor poate fi făcută grafic. Pentru aceasta, este suficient să construim un grafic al funcției F (x) și să determinăm segmentele pe care funcția F (x) are doar un punct de intersecție cu axa abscisei (intervale de izolare).
După determinarea intervalelor de izolare, se utilizează diferite metode de rafinare a rădăcinilor.
Metode de rafinare a radacinii
Considerăm că separarea rădăcinilor ecuației (1) este realizată și că o singură rădăcină este localizată pe segmentul de izolare [a, b], care trebuie rafinat cu eroarea e (figura 1).
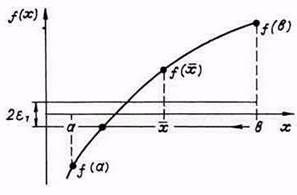
Figura 2. Metoda de dicotomie
Metoda de dihotomie, sau jumătate diviziune, este după cum urmează. Determinați mijlocul segmentului [a, b]. și calculați funcția. Apoi alegem care din cele două părți ale segmentului să ia pentru rafinarea ulterioară a rădăcinii. Dacă partea stângă a ecuației f (x) este o funcție continuă a argumentului x. atunci rădăcina va fi în jumătatea segmentului la capetele căruia f (x) are semne diferite. În Fig. 3 acesta va fi intervalul [a,], adică pentru pasul următor de rafinament se mișcă punctul b până la mijlocul segmentului și se continuă procesul de divizare ca și în segmentul inițial [a, b].
Procesul iterativ (repetat) va continua până când intervalul [a, b] devine mai mic decât eroarea specificată e:
sau când valorile funcției f (x) (reziduală) nu devin suficient de mici