
Acasă | Despre noi | feedback-ul
Sarcina principală a staticilor fermelor este utilizarea unor astfel de metode de calcul, care elimină soluția unui sistem de ecuații în comun.
Metoda punctelor de moment în cea mai simplă formă se aplică în fermele în care este posibilă tăierea numai a trei bare.
Determinarea forței O2. D2. U2 în elementele unei zăbrele structurate (Figura 1.4.1). Pre găsi reacția A și B. Secțiunea de sârmă nn trei eforturi tija sunt determinate și părți de acțiune fermă reprezintă vectorii respectivi O2. D2. U2 presupunând că eforturile sunt tensionate.
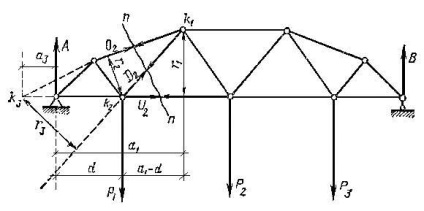
Având în vedere echilibrul părții stângi (în cazul în care există mai puține forțe), formăm trei ecuații, fiecare dintre acestea cuprinzând doar una necunoscută. Pentru aceasta, în loc de cele trei ecuații clasice: = 0, = 0, = 0, obținem pentru partea stângă a ecuației următoarea formă:
unde suma momentelor nu va include eforturile O2. D2 care trece prin punctul momentului k1. Suma momentelor nu conține forțele D2. U2; suma nu include eforturile O2, U2. Fiecare ecuație (1.4.1) va conține o singură forță necunoscută, ceea ce îl face ușor și precis să o găsească. Pentru a determina U2. compunem suma momentelor forțelor aplicate pe partea stângă a rampei de legătură, în raport cu punctul de intersecție al direcțiilor forțelor O2. D2:
Aici numărătorul este nimic ca timpul rămas (momentul de încovoiere în secțiunea transversală cu un imaginar grinzi de perete continuu) forțe externe în raport cu punctul k1.
unde Mvn k1 este momentul forțelor exterioare stânga față de punctul k1;
Acum, forța O2 este suma momentelor forțelor aplicate la partea stângă a fermei, relativ la punctul k2, punctul de dispariție D2. U2:
Pentru a determina forța D2, selectați punctul momentului k3 - punctul de intersecție al direcțiilor forțelor O2. Considerând echilibrul părții stângi, găsim
După cum vedem, atunci când aplicăm metoda punctelor de moment, forța este întotdeauna exprimată prin raportul momentului forțelor exterioare aplicate părții din stânga tăiată asupra brațului forței.
Astfel, pentru a determina forța U2 în elementul curelei inferioare a structurii semi-rasperului (figura 1.4.2), executăm o tăietură n - n ce intersectează patru bare.
Dar direcția celor trei eforturi este O2. V2 și V2 1 se intersectează în același punct. Considerăm că este momentul momentelor pentru determinarea U2:
În mod similar, forța O2 este determinată folosind punctul momentului k1.
O tăietură închisă este utilizată pentru a găsi forțe în puțul fermei Shukhov (Figura 1.4.3) și sisteme similare. Să presupunem că trebuie să determinăm forța O1. în primul element al centurii superioare a fermei lui Shukhov.
Pentru forțele definite în barele O1. O2 și O5 care leagă cele două triunghiuri principale, executăm o tăietură care taie tijele curelei superioare unul câte unul, iar bretelele D1 și D2 de două ori.
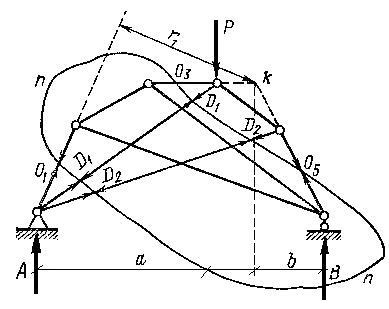
Luând în considerație echilibrul părții fermei situate în interiorul tăieturii, n-n. formează condiția de echilibru sub forma dispariției sumei momentelor în raport cu punctul k al intersecției liniilor axiale ale tijelor O2 și O5:
Metoda de proiecții se aplică atunci când punctul de moment este la infinit, adică atunci când două tije de trei disecții sunt paralele. Să presupunem că doriți să determinați forța în brațul fermei D3 cu curele paralele (Figura 1.4.4).
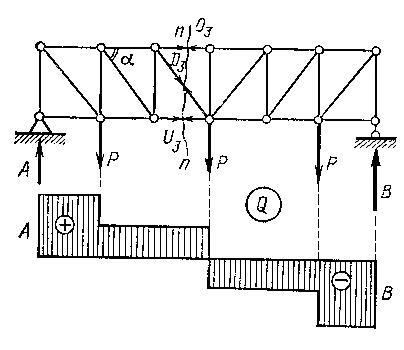
Realizarea tăieturii n-n. Discutăm trei bare, forțele în care se află O3. D3. U3. Direcția de efort O3 și U3. sunt paralele, deci punctul de moment pentru D3 va fi la infinit. Problema determinării forței D3 este ușor de rezolvat prin aplicarea ecuației proeminențelor tuturor forțelor aplicate părții tăiate la axa verticală perpendiculară pe direcțiile O3 și U3:
unde (A-P) = Qn este forța transversală în secțiunea fazei imaginare n-n cu un perete solid.
O structură de fermă cu curele paralele lucrează la percepția forței transversale. Legea schimbării forțelor din bretele este ușor de stabilit din diagrama forțelor transversale.
1.4.3 Metoda de tăiere a nodurilor.
Metoda de tăiere a nodurilor împreună cu metoda momentelor este una dintre cele mai comune metode de determinare a forțelor. Pentru fiecare nod al structurii, se formează două condiții de echilibru sub forma a două ecuații de proiecție în două axe neparalel. Prin urmare, este recomandabil să începeți cu un nod în cazul în care doi
rod. Prezentăm aplicarea metodei de tăiere a nodurilor pentru determinarea forțelor în elementele structurii din fig. 1.4.5, a. Pentru a determina Forța O, cea mai ușoară cale este de a tăia nodul de susținere al structurii (Figura 1.4.5.6).
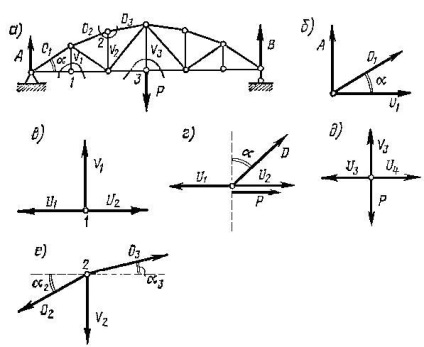
Proiectând toate forțele care acționează asupra nodului, pe verticală obținem:
adică, forța din elementul de susținere al centurii superioare a structurii este proporțională cu reacția de referință.
Pentru a determina eforturile V1 și V2 rafturi, respectiv, tăiate nodurile 1 și W coardei inferioare. și proiectarea tuturor forțelor aplicate pe un ax vertical, obținem (Figura 1.4.5 in.) V1 = 0. Aceasta conduce la următoarea concluzie: în cazul în care trei bar converg la un nod, dintre care două au aceeași direcție (U1 și U2) și nu există nici o sarcină, forța în direcția singur tijei (V1) este egal cu zero. O astfel de tijă este numită zero. Această regulă se aplică și la nodurile cărora li se aplică de sarcină, având în nici o componentă care este normal la celelalte două tije de aceeași direcție.
Să presupunem că nodul în care converg două talie forțele U1 și U2 și forța aplicată în D. oblici forța orizontală F (Fig. 1.4.5, d). Proiectând toate forțele care acționează asupra nodului, pe verticală, găsim: