Unul dintre subiectele care necesită atenție maximă și perseverență din partea studenților este soluția inegalităților. Acestea sunt similare cu ecuațiile și sunt foarte diferite de ele. Pentru că au nevoie de o abordare specială pentru rezolvarea lor.
Proprietățile care vor fi necesare pentru a găsi răspunsul
Toate acestea sunt folosite pentru a înlocui înregistrarea existentă cu echivalentul. Cele mai multe dintre ele sunt similare cu cele din ecuații. Dar există diferențe.
- O funcție definită în DGD sau orice număr poate fi adăugată la ambele părți ale inegalității inițiale.
- În mod similar, multiplicarea este posibilă, dar numai o funcție pozitivă sau un număr.
- Dacă această acțiune este efectuată cu o funcție sau un număr negativ, atunci semnul inegalității trebuie înlocuit cu cel opus.
- Funcțiile care nu sunt negative se pot ridica la un nivel pozitiv.
Uneori soluția de inegalități este însoțită de acțiuni care oferă răspunsuri externe. Acestea trebuie eliminate prin compararea domeniului SGD și a setului de soluții.
Utilizând metoda intervalului
Esența lui este de a reduce inegalitatea la o ecuație în care partea dreaptă este zero.
- Determinați zona în care se află valorile admise ale variabilelor, adică DGS.
- Transformați inegalitatea folosind operațiile matematice, astfel încât să existe un zero în partea sa dreaptă.
- Înlocuim semnul inegalității cu "=" și rezolvăm ecuația corespunzătoare.
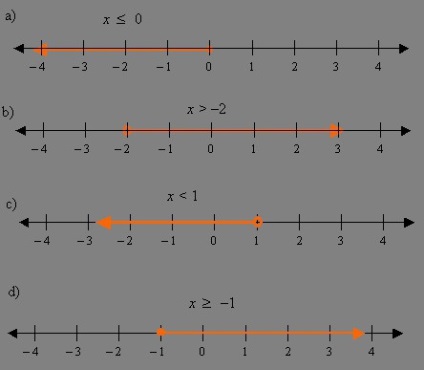
- Pe axa numerică, notați toate răspunsurile obținute în timpul deciziei, precum și intervalele LDZ. Cu inegalitate strictă, punctele trebuie să fie perforate. Dacă există un semn egal, atunci ar trebui să fie pictat peste.
- Determinați semnul funcției inițiale pe fiecare interval obținut din punctele DGD și împărțind răspunsurile sale. Dacă semnul unei funcții nu se schimbă atunci când trece printr-un punct, intră în răspuns. În caz contrar, este exclusă.
- Punctele de frontieră pentru punctul LDZ trebuie să fie verificate suplimentar și numai apoi incluse sau nu ca răspuns.
- Răspunsul obținut trebuie să fie scris sub formă de seturi combinate.
Un pic despre dubla inegalitate
Ei folosesc în înregistrare imediat două semne de inegalitate. Adică, o anumită funcție este limitată de condițiile de două ori. Aceste inegalități sunt rezolvate ca un sistem de două, atunci când originalul este împărțit în părți. Și în metoda intervalului sunt indicate răspunsurile din soluția celor două ecuații.
Pentru a le rezolva, este permisă utilizarea proprietăților indicate mai sus. Cu ajutorul lor, este convenabil să reducem inegalitatea la zero.

Cum sunt lucrurile cu inegalitățile în care există un modul?
În acest caz, soluția inegalităților folosește următoarele proprietăți și acestea sunt valabile pentru o valoare pozitivă a "a".
Dacă "x" are o expresie algebrică, atunci astfel de substituții sunt valide:
Dacă inegalitățile nu sunt stricte, atunci formulele sunt de asemenea adevărate, numai în ele, în plus față de semn mai mult sau mai puțin, apare "=".
Cum se rezolvă sistemul de inegalități?
Aceste cunoștințe sunt necesare în cazurile în care se dă o astfel de sarcină sau există o înregistrare a unei inegalități duble sau un modul a apărut în înregistrare. Într-o astfel de situație, soluția va fi acele valori ale variabilelor care satisfac toate inegalitățile din notație. Dacă nu există astfel de numere, atunci sistemul de soluții nu.
Planul prin care soluția sistemului de inegalități este îndeplinită:
- rezolva fiecare dintre ele separat;
- reprezintă toate intervalele pe axa numerică și determină intersecțiile lor;
- înregistrați răspunsul sistemului, care va fi unirea a ceea ce sa întâmplat în al doilea paragraf.
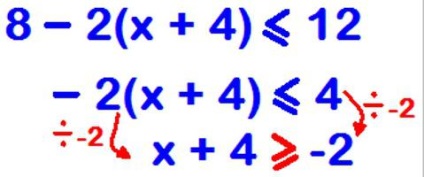
Cum rămâne cu inegalitățile fracționare?
Întrucât la momentul deciziei lor ar putea fi necesar să se schimbe semnul inegalității, este necesar să urmăriți cu atenție și cu atenție toate punctele din plan. În caz contrar, puteți obține răspunsul opus.
Soluția de inegalități fracționate utilizează, de asemenea, metoda intervalului. Iar planul de acțiune va fi:
- Folosind proprietățile descrise, pentru a oferi fracțiunilor o astfel de formă încât în dreapta semnului să rămână numai zero.
- Înlocuiți inegalitatea cu "=" și stabiliți punctele în care funcția va fi zero.
- Marcați-le pe axa de coordonate. În acest caz, numerele rezultate din calculele din numitor vor fi întotdeauna perforate. Toate celelalte se bazează pe condiția de inegalitate.
- Definiți intervalele constantei semnelor.
- Ca răspuns, scrieți unirea acelor intervale, semnul căruia corespunde celui care se afla în inegalitatea inițială.
Situații în care iraționalitatea apare în inegalitate
Cu alte cuvinte, intrarea are o rădăcină matematică. Deoarece în cursul școlii de algebră majoritatea sarcinilor sunt pentru rădăcina pătrată, atunci ea va fi luată în considerare.
Soluția inegalităților iraționale reduce la obținerea unui sistem de două sau trei care va fi echivalent cu cel original.
Exemple de soluții de diferite tipuri de inegalități
Pentru a adăuga claritate teoriei soluționării inegalităților, sunt prezentate mai jos exemple.
Primul exemplu. 2x - 4> 1 + x
Soluția: pentru a determina LDU, este suficient doar să ne uităm îndeaproape la inegalitate. Se formează din funcții liniare, deci este definită pentru toate valorile variabilei.
Acum este necesar să se scadă (1 + x) de ambele părți ale inegalității. Se obține: 2 - 4 - (1 + x)> 0. După paranteze sunt dezvăluite și termeni similari sunt date inegalitate ia forma: x - 5> 0.
Ecuating la zero, este ușor să găsiți soluția sa: x = 5.
Acum, acest punct cu numărul 5, trebuie notat pe fascicul de coordonate. Apoi verificați semnele funcției originale. În primul interval de la minus infinit la 5 putem lua numărul 0 și îl înlocuim în inegalitatea obținută după transformări. După calcule, se obține -7> 0. sub arcul intervalului, trebuie să semnați un semn minus.
În intervalul următor de la 5 la infinit, putem alege numărul 6. Apoi se pare că 1> 0. Semnul "+" este semnat sub arc. Acest al doilea interval este răspunsul inegalității.
Răspuns: x se află în intervalul (5; ∞).
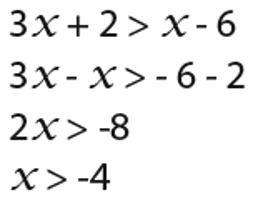
Cel de-al doilea exemplu. Este necesară rezolvarea unui sistem de două ecuații: 3x + 3 ≤ 2x + 1 și 3x - 2 ≤ 4x + 2.
Soluția. ODZ-ul acestor inegalități se află, de asemenea, în intervalul oricărui număr, dat fiind funcțiile liniare.
Apoi este necesar să acționăm pas cu pas. În primul rând, transformați prima inegalitate și echivalați-o cu zero. 3x + 3 - 2x - 1 = 0. Asta este, x + 2 = 0. Astfel, x este -2.
A doua inegalitate ia forma unei astfel de ecuații: 3x - 2 - 4x - 2 = 0. După transformare: -x - 4 = 0. Din aceasta, valoarea variabilei este -4.
Aceste două numere trebuie marcate pe axă, prin spațiere. Deoarece inegalitatea nu este strictă, toate punctele trebuie să fie pictate. Primul interval este de la minus infinit la -4. Lăsați numărul -5 să fie aleasă. Prima inegalitate dă o valoare de -3, iar cea de-a doua. Prin urmare, acest interval nu intră în răspuns.
Al doilea interval este de la -4 la -2. Puteți alege un număr -3 și îl puteți înlocui în ambele inegalități. Primul și al doilea rezultat sunt -1. Prin urmare, sub arc "-".
În ultimul interval de la -2 la infinit, cel mai bun număr este zero. Este necesar să o înlocuiți și să găsiți valorile inegalităților. În primul dintre ele se obține un număr pozitiv, iar al doilea este zero. Acest decalaj trebuie, de asemenea, să fie exclus din răspuns.
Dintre cele trei intervale, numai una este soluția inegalității.
Răspuns: x aparține lui [-4; -2].
Cel de-al treilea exemplu. | 1 - x |> 2 | x - 1 |.
Soluția. Primul lucru pe care trebuie să-l faceți este să determinați punctele la care funcțiile merg la zero. Pentru stânga, acest număr va fi 2, pentru cel de dreapta - 1. acestea ar trebui să fie notate pe rază și să determine intervalele de semn-constantă.
În primul interval, de la minus infinit la 1, funcția de pe partea stângă a inegalității ia valori pozitive, iar din partea dreaptă negativă. Sub arc, trebuie să scrieți două semne "+" și "-" unul lângă celălalt.
Următorul interval este de la 1 la 2. Pe ambele funcții iau valori pozitive. Deci sub arc există două plusuri.
Al treilea interval de la 2 la infinit va da un astfel de rezultat: funcția stângă este negativă, cea dreaptă este pozitivă.
Luând în considerare semnele rezultate, este necesar să se calculeze valorile inegalității pentru toate lacunele.
Pe prima, obținem următoarea inegalitate: 2 - x> -2 (x - 1). Minusul înainte de cei doi în a doua inegalitate se datorează faptului că această funcție este negativă.
După transformare, inegalitatea arată astfel: x> 0. Acesta oferă imediat valorile variabilei. Asta este, din acest interval doar intervalul de la 0 la 1 va răspunde.
Pe al doilea: 2 - x> 2 (x - 1). Transformările vor da următoarea inegalitate: -3x + 4 mai mare decât zero. Valoarea lui zero va fi valoarea x = 4/3. Având în vedere semnul inegalității, se dovedește că x trebuie să fie mai mic decât acest număr. Prin urmare, acest interval este redus la intervalul de la 1 la 4/3.
Aceasta din urmă dă următoarea inegalitate: - (2 - x)> 2 (x - 1). Transformarea lui duce la aceasta: -x> 0. Aceasta este, ecuația este adevărată pentru x mai mică decât zero. Aceasta înseamnă că inegalitatea nu oferă soluții la intervalul necesar.
În primele două intervale, numărul 1 a fost limita. Trebuie verificat separat. Aceasta este, înlocuiți în inegalitatea inițială. Se pare că | 2 - 1 |> 2 | 1 - 1 |. Numărătoarea dă că 1 este mai mare decât 0. Aceasta este o afirmație adevărată, deci unitatea este inclusă în răspuns.
Răspuns: x se află în intervalul (0; 4/3).