FUNCȚII TRIGONOMETRICE
Semnificația geometrică a egalității este văzută în fig. 11. Aici x este jumătatea arcului AB, iar păcatul x este jumătatea coardei corespunzătoare. Evident, pe măsură ce punctele A și B se apropie reciproc, lungimea coardei se apropie de lungimea arcului tot mai precis. Din aceeași figură, este ușor să se deducă inegalitatea
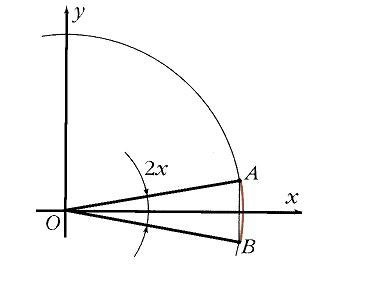
Formula (*) a matematicii este numită o limită remarcabilă. Din aceasta, în special, rezultă că păcatul xx pentru micul x.
Funcțiile y = tan x, y = ctg x. Două alte funcții trigonometrice - tangente și cotangente sunt cel mai simplu definite ca relația dintre sinele și cosinusul deja cunoscut:
Ca sinus și cosinus, tangenta și cotangentul sunt funcții periodice, dar perioadele lor sunt egale cu p. și anume ele sunt jumătate din dimensiunea sinusului și cosinusului. Motivul pentru acest lucru este clar: dacă sinele și cosinusul schimbă semnele, atunci raportul lor nu se va schimba.
Deoarece există un cosinus în numitorul tangent, tangenta nu este definită în acele puncte unde cosinusul este 0, când x = p / 2 + k p. În toate celelalte puncte, crește în mod monoton. Liniile drepte x = p / 2 + k p pentru tangenta sunt asimptote verticale. În punctele k p, tangenta și panta sunt 0 și respectiv 1 (Figura 12).
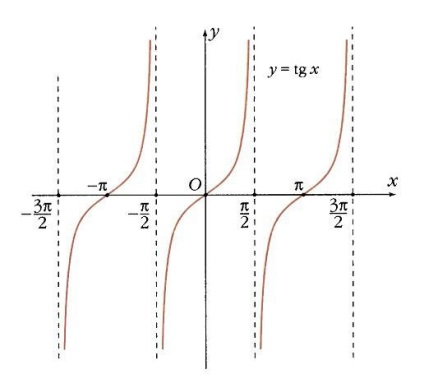
Cotangent nu este definit în cazul în care sinusul este 0 (atunci când x = k p). În alte puncte scade monotonic, iar liniile x = k p sunt asimptotele sale verticale. La punctele x = p / 2 + k p, cotangenta devine 0, iar coeficientul unghiular la aceste puncte este -1 (Figura 13).
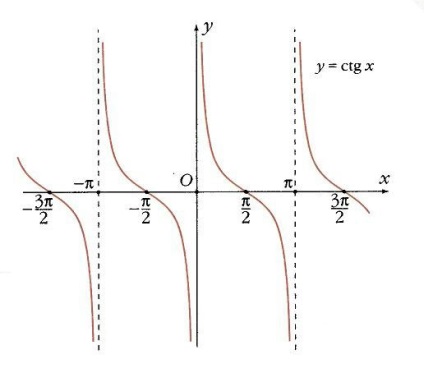
Paritate și periodicitate.
Se spune că o funcție este chiar dacă f (-x) = f (x). Funcțiile cosinus și secante sunt uniforme, iar sinus, tangent, cotangent și cosecant sunt funcții ciudate:
sin (-α) = - sin α
tg (-α) = - tan α