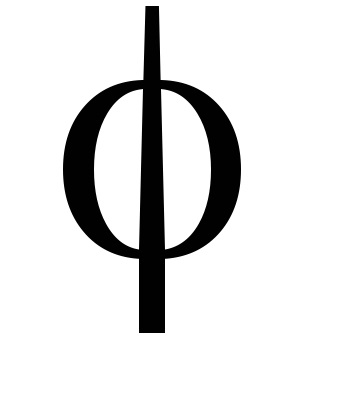
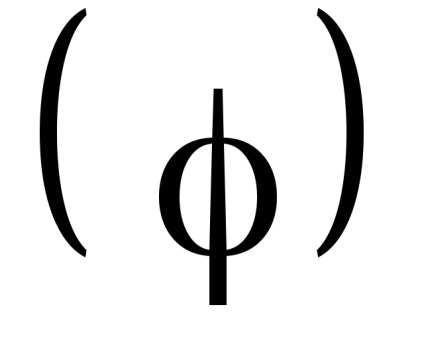
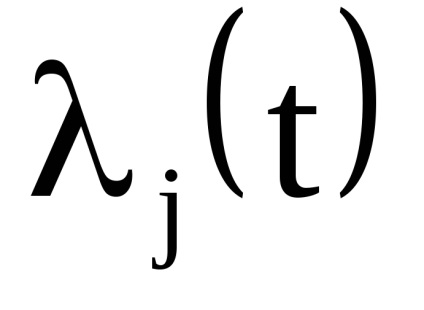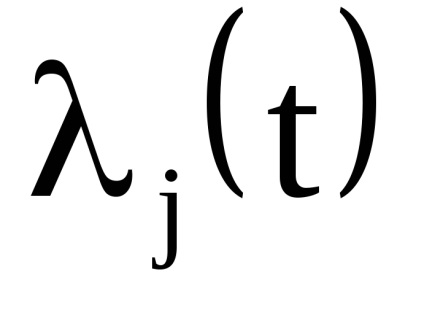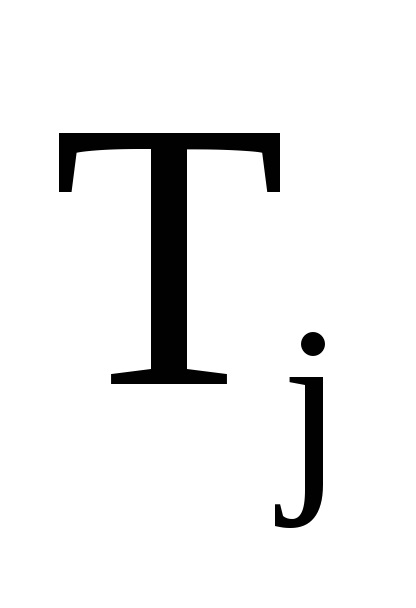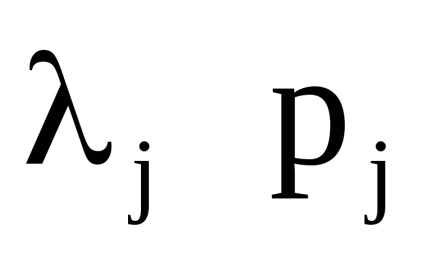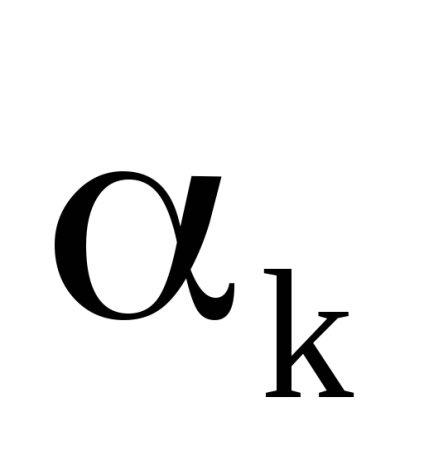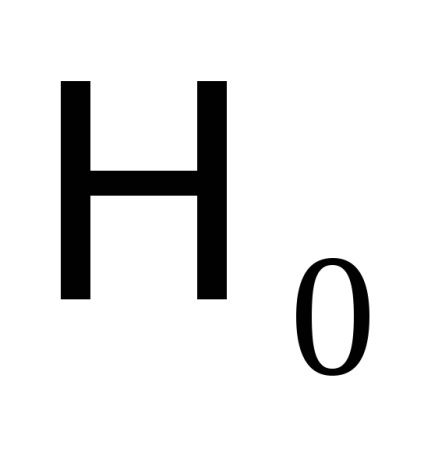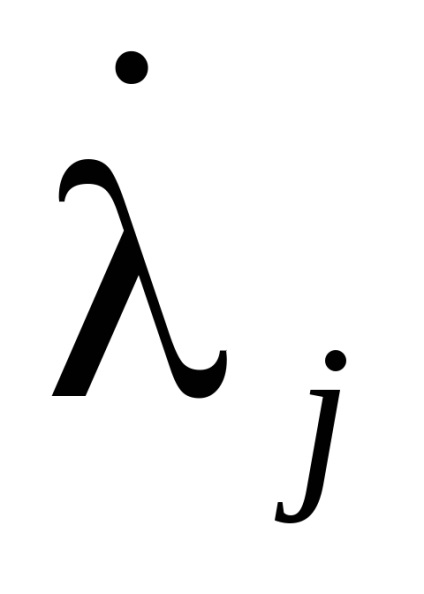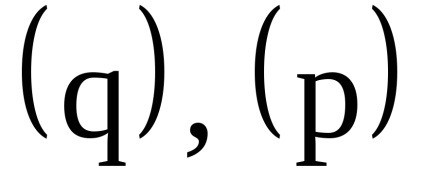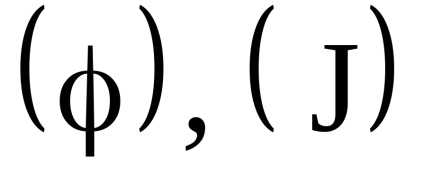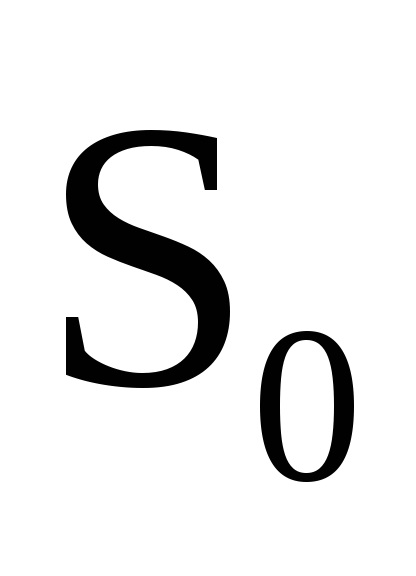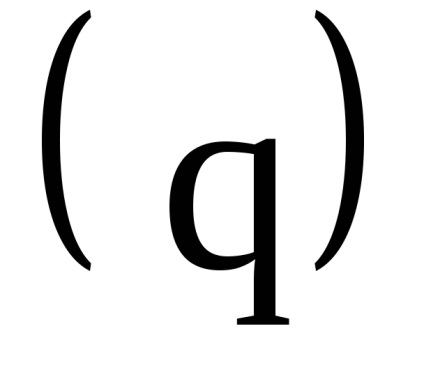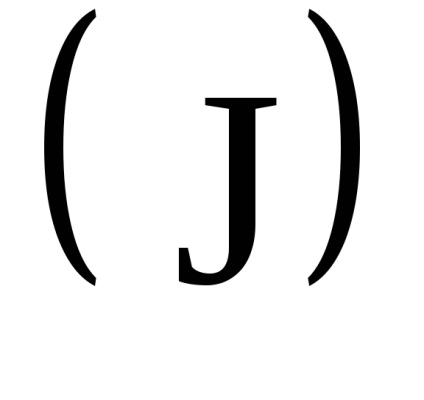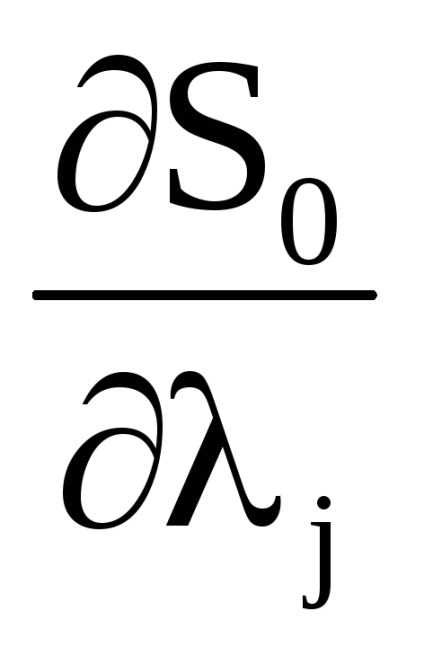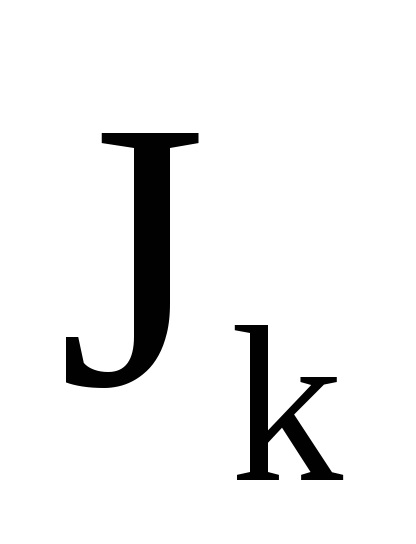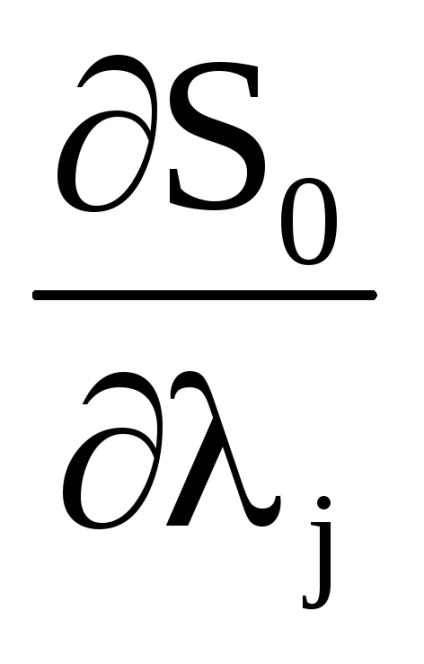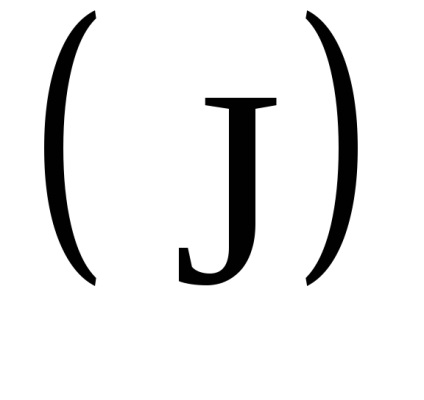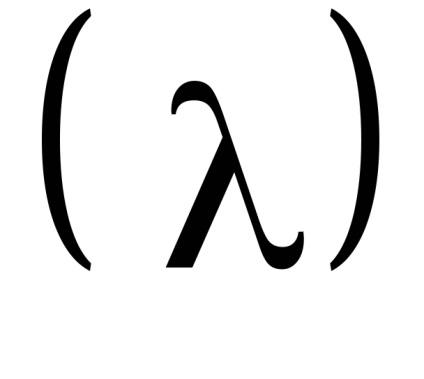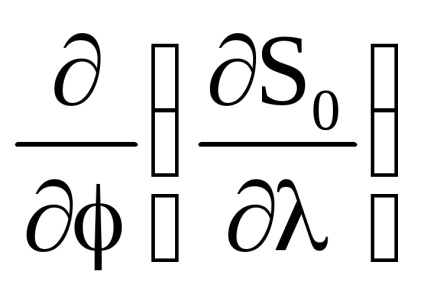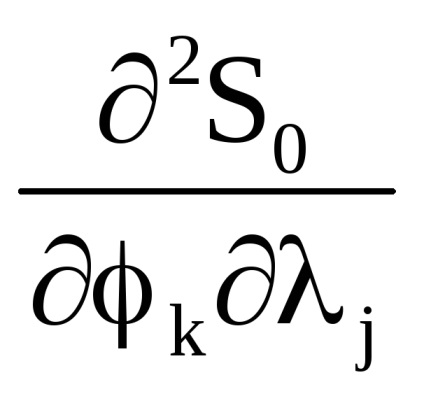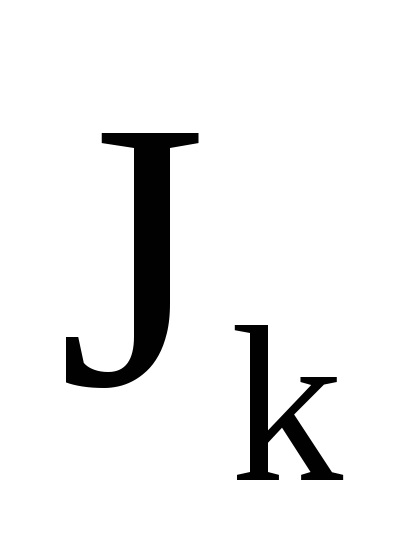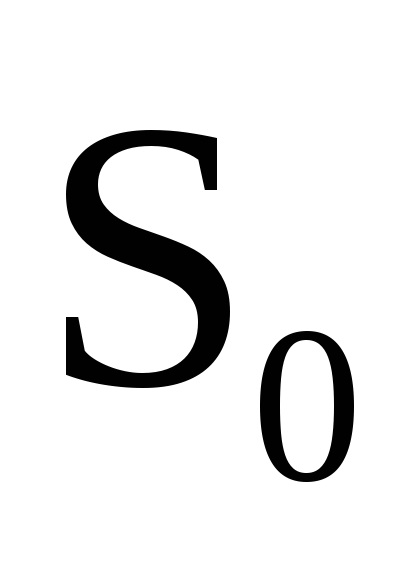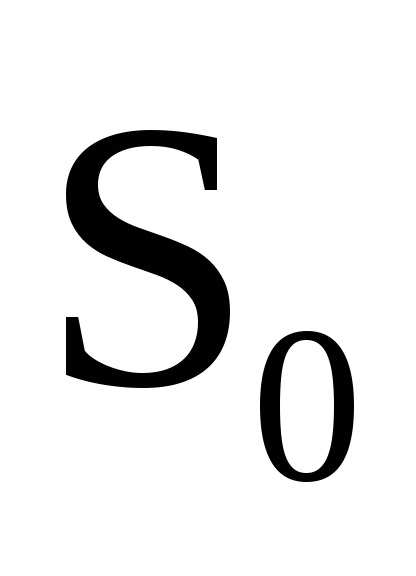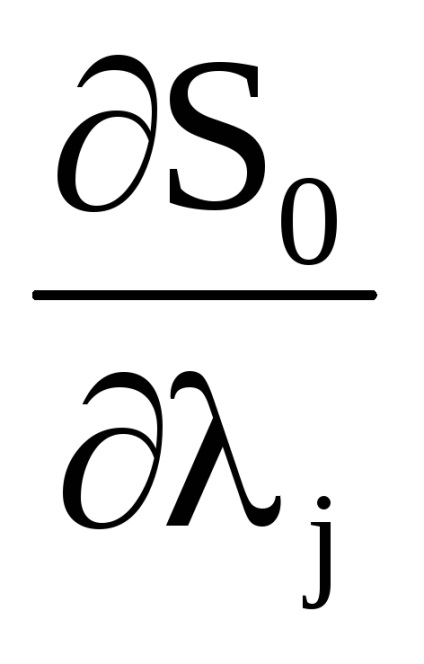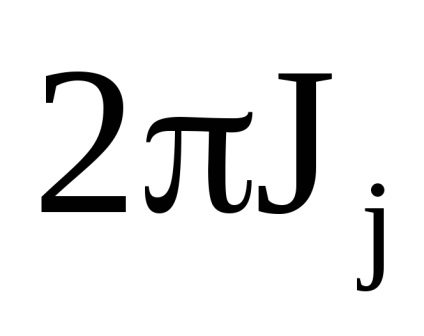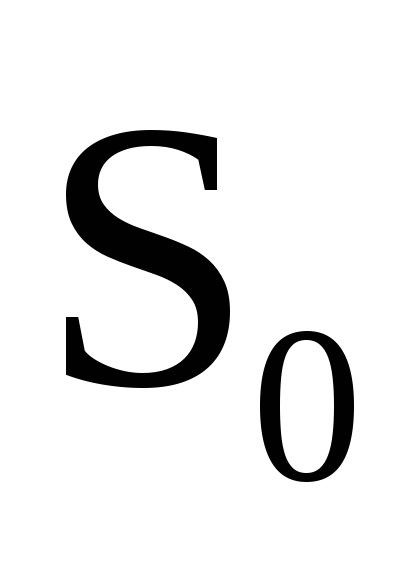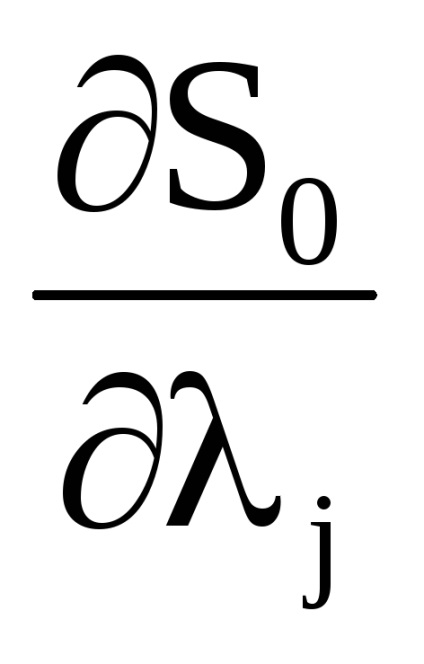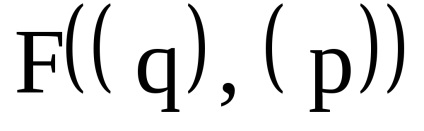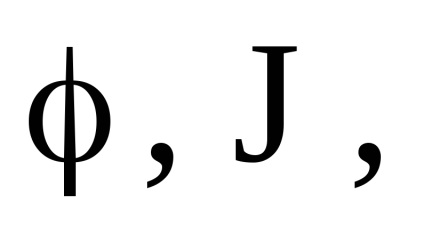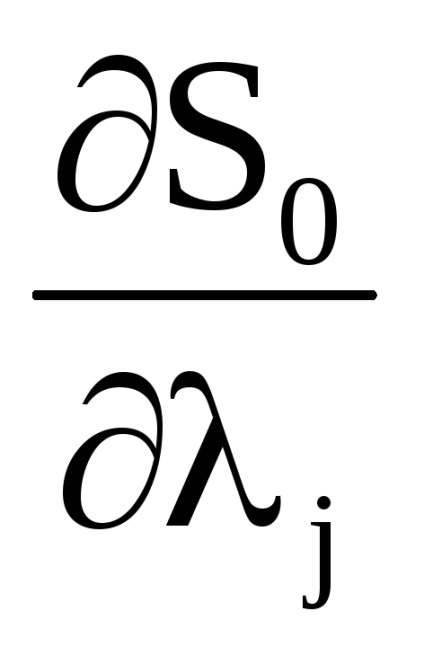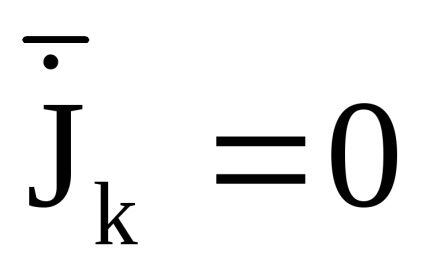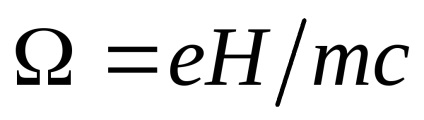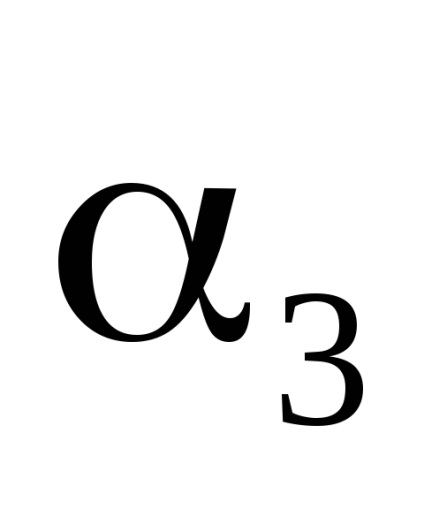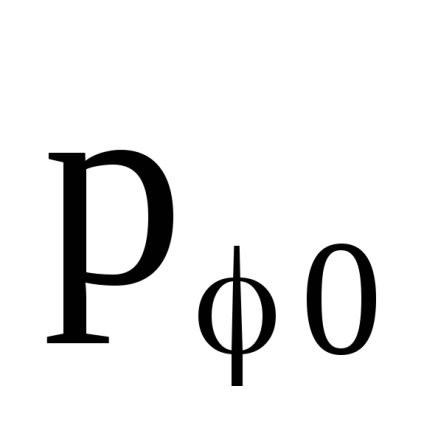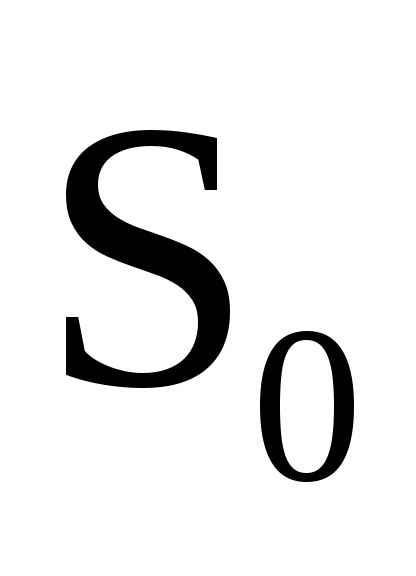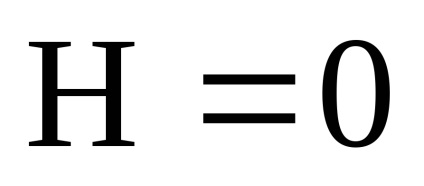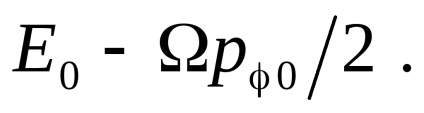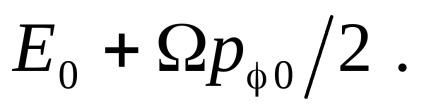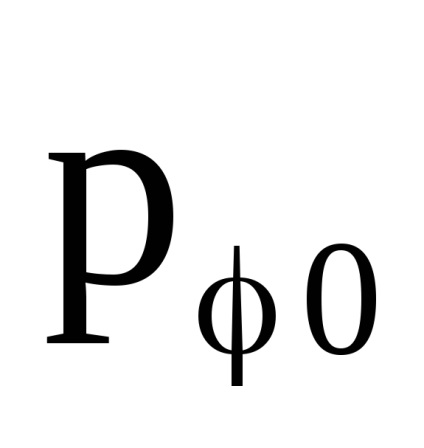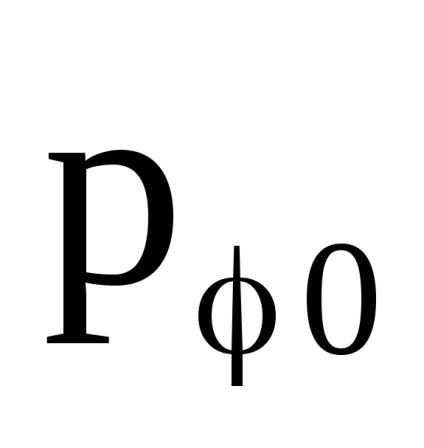O proprietate importantă a variabilelor de acțiune este proprietatea invarianței adiabatice, care constă în faptul că variabilele de acțiune păstrează valorile lor constante, iar în acele cazuri în care hamiltonianul sistemului depinde de timpul prin intermediul unor parametri
, care, așa cum se spune, se schimbă adiabatic cu timpul, adică foarte încet. Prin lent înseamnă astfel de schimbări, sub care putina schimbare pentru perioade de timp, egala in ordinea marimii cu perioadele , care este,Este clar că astfel de sisteme mecanice nu sunt strict izolate. Arătăm că variabilele de acțiune în astfel de sisteme sunt invariante adiabatice.
Luați în considerare un sistem care coincide în fiecare moment cu sistemul conservator studiat mai sus, care permite o separare completă a variabilelor. Presupunem de asemenea că mișcarea sistemului este finită. Hamiltonianul unui astfel de sistem depinde în mod evident de parametrii
, care îndeplinesc condițiile (61.11); acesta poate fi reprezentat în formă
Cu constanta
sunt funcții periodice ale coordonatelor corespunzătoare ; în acest caz sunt funcții periodice ale timpului.
Dacă parametrii
schimba lent în timp, în ciuda faptului că sistemul descris de hamiltonianul (62,11) nu este conservatoare, soluția ecuației Hamilton-Jacobi poate fi solicitată într-o formă aproape (24,11):
unde, totuși, parametrii
, și, prin urmare, cantitățile și schimbă încet cu timpul. Înlocuind (63.11) în ecuația Hamilton-Jacobi și neglijând în ea termeni proporțional cu , obținem ecuația aproximării "zeroth"
Prin (61.11), această ecuație poate fi rezolvată prin asumarea tuturor
sunt constante și numai în soluțiile construite ele sunt considerate a fi funcții date de timp. Prin urmare, toate formulele obținute mai sus pentru sistemul conservator rămân valabile, dar toate relațiile includ acum parametrii dependenți de timp .
Funcția de generare a transformării canonice de la variabile
la variabile este determinată de funcție , care acum, totuși, va depinde :
Observăm asta
depinde, de asemenea .
Se scriu formulele pentru transformarea canonică generată de funcție (65.11):
Noile ecuații de mișcare au forma
În toate formulele diferențierea cu privire la
Ar trebui făcută constant și ; după diferențiere, substituția (67.11) și derivații din formulele (69.11), (70.11) sunt exprimate prin.
Pentru a demonstra proprietatea invarianței adiabatice a variabilelor
În medie, ecuațiile (70.11) într-un interval de timp care este mic în comparație cu timpul unei modificări notabile a parametrilor și suficient de mare în comparație cu perioadele sistemului. Cu o astfel de alegere a intervalului de timp, (din cauza schimbării lente ) poate fi scos din sub semnul mijlocului. Prin urmare,
Acum arătăm că derivatele
sunt funcții periodice cu valoare unică . Dacă este așa, atunci ele pot fi descompuse în serii Fourier, coeficienții cărora vor depinde și . La rândul său, seria Fourier pentru derivate nu vor conține termeni constanți și, prin urmare, atunci când medierea pe un interval de timp suficient de mare, toate instrumentele derivate Invarianta adiabatică a tuturor va fi dovedit.
Observăm asta
- funcția ambiguă a coordonatelor , deoarece în conformitate cu (66.11) ea poate fi reprezentată în formă
Pentru întreaga perioadă de schimbare a coordonatelor
(pentru restul fix) incrementat
funcții
- funcțiile unice ale coordonatelor, deoarece în diferențierea cu privire la aditivi, multipli , care duc la ambiguitate , va dispărea. deoarece - funcții unice ale coordonatelor , atunci ele sunt funcții periodice ale variabilelor unghiulare ; aceste funcții nu își vor schimba valorile atunci când se schimbă pe (pentru valori date ). Cu alte cuvinte, orice funcție unică , exprimată în termeni de variabile canonice este o funcție periodică a fiecăruia cu o perioadă egală cu . Deci toate sunt funcții periodice cu valoare unică . Am arătat mai sus că în acest caz totul și, prin urmare, toate
Se dovedește proprietatea invarianței adiabatice a tuturor variabilelor de acțiune.
Un exemplu. Cum se va schimba energia unei particule încărcate e de masă m în câmpul central U (r) atunci când câmpul magnetic slab omogen de intensitate H este pornit lent?
Se scrie funcția Hamilton a unei încărcări într-un sistem de coordonate sferice (axa Oz a unui sistem de coordonate cartezian este paralelă cu H):
aici
- viteza luminii. Prin condiția problemei, câmpul magnetic este slab și, prin urmare, ultimul termen (quadratic în H) este neglijat.
Ecuația Hamilton-Jacobi ia în considerare acest lucru
unde
- energia particulelor, -ciclotronice.
Se caută soluția în formă
Aici, ca o constantă
am ales . substituind în (74.11), obținem
Ecuația (75.11) definește funcția necesară pentru a calcula variabila de acțiune
:
în mod evident,
va coincide cu , calculată pentru caz , dacă în ultima expresie, în loc de înlocuiți o combinație Prin urmare, cantitatea rămâne constant atunci când câmpul magnetic omogen este pornit lent. În afară de aceasta, cantitatea - componentă a impulsului generalizat de încărcare. Conform sensului fizic - Proiecția conservată a momentului unghiular al sarcinii pe vectorul H.
Articole similare