Secvența Fibonacci este o serie de numere în care fiecare număr succesiv este egal cu suma celor două numere anterioare. Secvențele numerice sunt adesea găsite în natură și artă sub formă de spirale și "secțiune de aur". Cea mai ușoară modalitate de a calcula secvența Fibonacci este de a crea o tabelă, dar această metodă nu este aplicabilă secvențelor mari. De exemplu, dacă doriți să determinați cel de-al 100-lea membru al unei secvențe, este mai bine să utilizați formula Binet.
Etapele Editare
Metoda 1 din 2:
Editarea tabelului


- De exemplu, dacă doriți să găsiți al cincilea număr al unei secvențe, desenați un tabel cu cinci rânduri.
- Folosind masa, nu puteți găsi un număr aleatoriu fără a calcula toate numerele anterioare. De exemplu, dacă doriți să găsiți numărul 100 al unei secvențe, trebuie să calculați toate numerele: de la primul la cel de-al 99-lea. Prin urmare, tabelul este valabil numai pentru găsirea primelor numere ale secvenței.
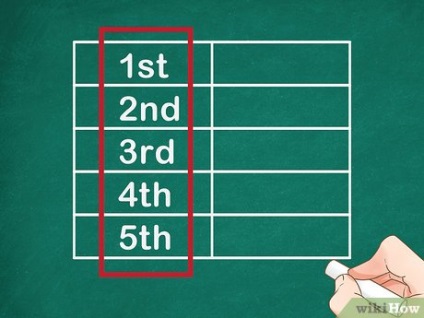

- Astfel de cifre definesc numerele de ordine ale numerelor de secvență Fibonacci (numere).
- De exemplu, dacă doriți să găsiți al cincilea număr al unei secvențe, scrieți următoarele numere în coloana din stânga: 1, 2, 3, 4, 5. Asta înseamnă că trebuie să găsiți numărul 1 până la al cincilea al secvenței.


- Rețineți că secvența Fibonacci începe întotdeauna cu 1. Dacă secvența începe cu un alt număr, ați calculat incorect toate numerele până la prima.


- Rețineți: pentru a găsi un număr din secvența Fibonacci, trebuie doar să adăugați cele două numere anterioare.
- Pentru a crea o secvență, nu uitați de 0, care se află înaintea lui 1 (primul membru), deci 1 + 0 = 1.


- 1 + 1 = 2. Al treilea termen este 2.


- 1 + 2 = 3. Al patrulea termen este de 3.


- 2 + 3 = 5. Al cincilea termen este de 5.
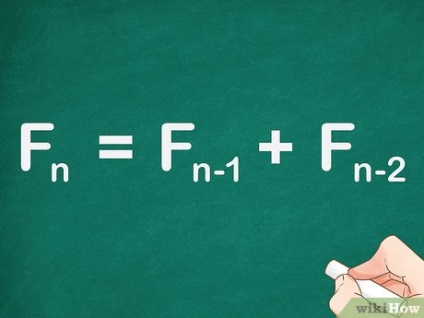
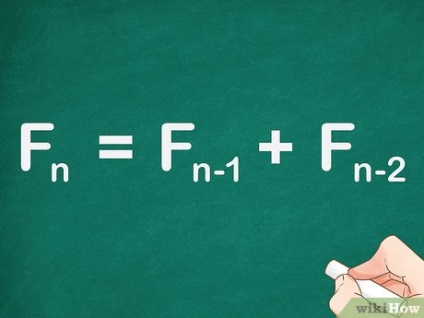
Adăugați cele două numere anterioare pentru a găsi un număr din secvența Fibonacci. Această metodă se bazează pe formula: F n = F n - 1 + F n - 2 = F_ + F_>. [1] Această formulă nu este închisă, prin urmare, cu ajutorul acestei formule, nu se poate găsi nici un membru al secvenței fără a se calcula toate numerele anterioare.
Metoda 2 din 2:
Formula Binet și secțiunea de aur Edit href = Edit
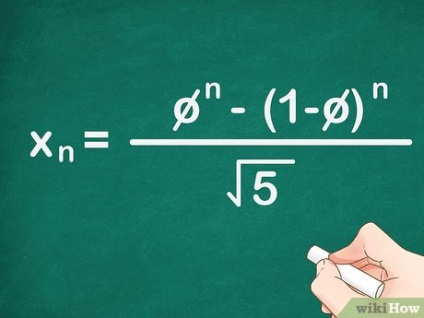
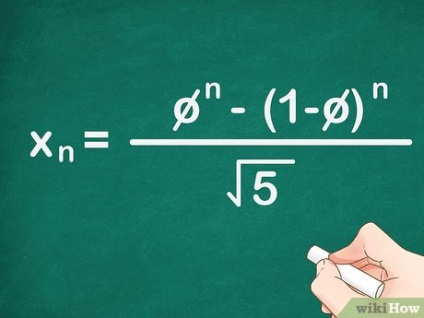
- Aceasta este o formulă închisă, deci orice membru al secvenței poate fi găsit din ea fără a calcula toate numerele anterioare.
- Aceasta este o formulă simplificată derivată din formula Binet pentru numerele Fibonacci. [3]
- Formula are o secțiune de aur (φ), deoarece raportul oricărui număr consecutiv al secvenței Fibonacci este foarte similar cu raportul de aur. [4]
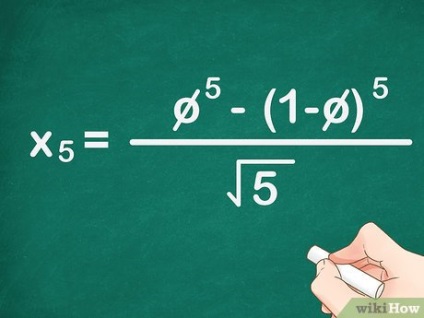
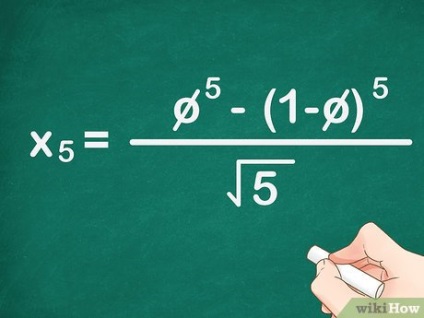
- De exemplu, dacă doriți să găsiți al cincilea număr al unei secvențe, înlocuiți formula din formula 5. Formula este scrisă ca: x 5> = φ 5 - (1 - φ) 5 5 - (1- \ phi) >>>>.
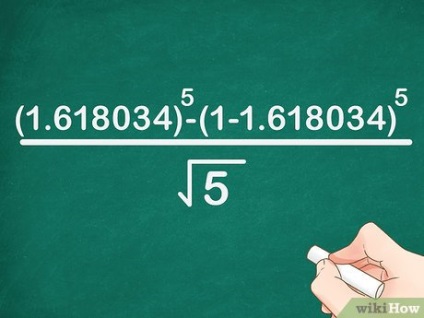
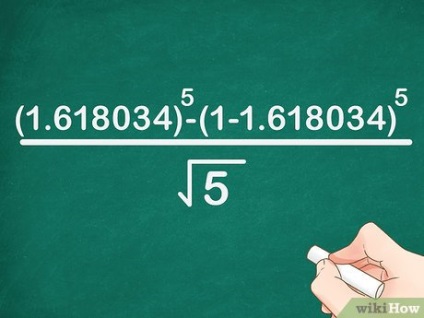
- De exemplu, dacă doriți să găsiți al cincilea număr al unei secvențe, formula va fi scrisă astfel: x 5> = (1. 618034) 5 - (1 - 1. 618034) 5 5 - (1-1.618034) ^ >>>>.
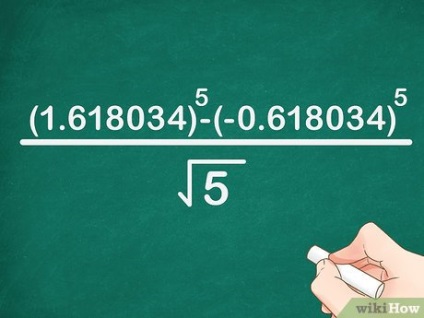
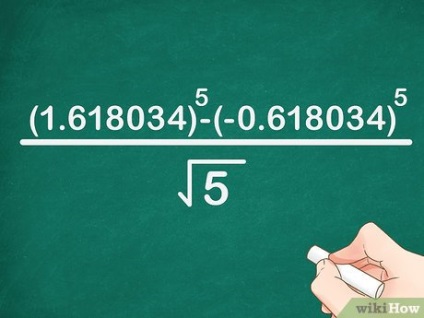
- În exemplul nostru, formula este scrisă ca: x 5> = (1. 618034) 5 - (- 0. 618034) 5 5 - (- 0,618034) ^ >>>>.
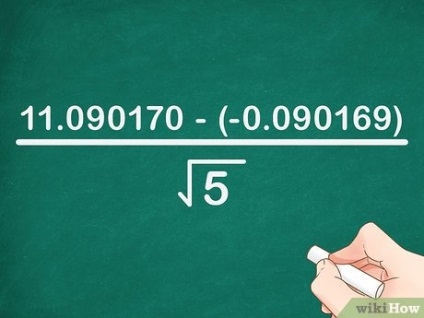
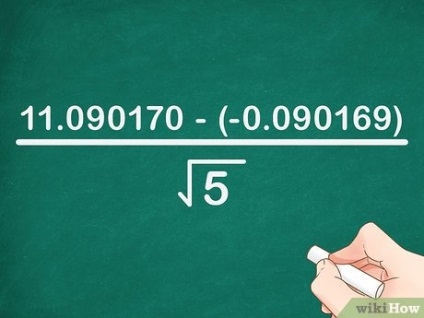
- În exemplul nostru: 1. 618034 5 = 11. 090170 = 11.090170>; - 0. 618034 5 = -0,090169 = -0,090169>. Formula va fi scrisă după cum urmează: x 5 = 11. 090170 - (- 0. 090169) 5 = >>>.
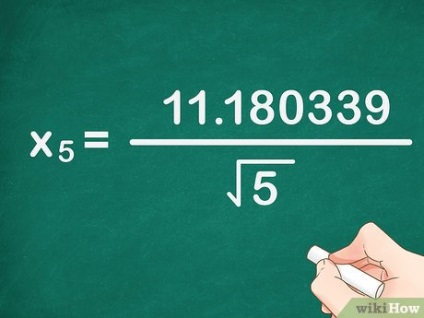
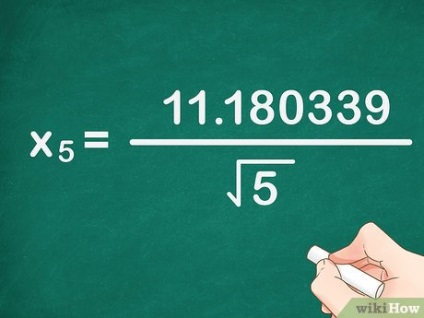
- În exemplul nostru: 11. 090170 - (- 0. 090169) = 11. 180339. Formula este după cum urmează: x 5> = 11. 180339 5 >>>.
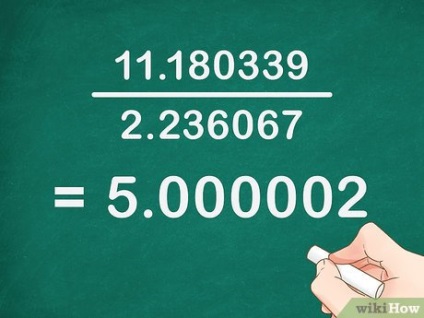
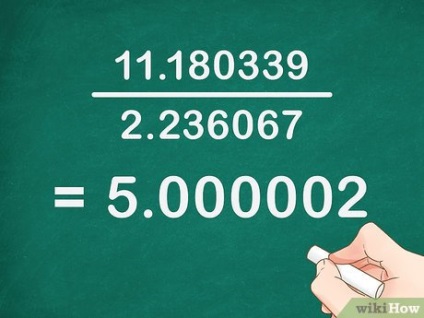
- În exemplul nostru: 11. 180339 2. 236067 = 5. 000002> = 5,000002>.


- Dacă utilizați cifre din jur în calculele dvs., veți obține un număr întreg. Lucrul cu numerele rotunjite este mult mai ușor, dar în acest caz veți obține o fracție zecimală. [6]
- În exemplul nostru, aveți o fracție zecimală de 5,000002. Rotiți-l până la cel mai apropiat număr întreg și obțineți al cincilea număr de secvență Fibonacci, care este 5.