Este - în avion. Deoarece există o sarcină geodezică directă și inversă pe elipsoidul pământului. Va trebui să le rezolvați în cursul "Geodeziei superioare". Apoi veți ști diferența mare. Curbura Pământului, forma sa va face să se simtă.
Numele de sarcini geodezice "directe" și "inverse" sunt oarecum arbitrare, dar acum acceptate în mod tradițional în domeniul geodeziei și al măsurării geografice o dată pentru totdeauna. Doar una dintre problemele numite o linie dreaptă, în rezolvare care găsește coordonatele punctelor din teren, iar cealaltă - inversă, în rezolvarea ...
Să nu fugim.
Problema geodezică directă.
Spuneți-ne coordonatele punctului 1 (X1.Y1), poziția orizontală a liniei 1-2 d12 și unghiul de direcție # 945; 12 (Figura 7.3). Este necesar să găsiți coordonatele punctului 2. Acestea sunt condițiile problemei geodezice directe.
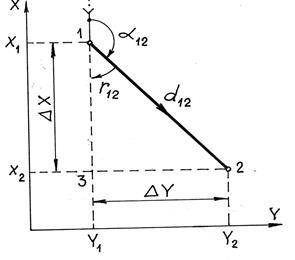
Fig. 7.3. Probleme geodezice directe și inverse în avion.
O sarcină geodezică directă este utilizată pentru a determina coordonatele punctelor de teren, în special în determinarea coordonatelor punctelor cursurilor teodolitice. Deoarece această problemă este rezolvată pe un plan (în proiecția Gauss-Krueger), triunghiul 123 este dreptunghiular. Linia 1-2 este orientată (în figură) în sistemele circulare (# 945;) și trimestrul (r). parametrii # 916; X și Y sunt numite incremente de coordonate. Pe baza geometriei și a sistemului de coordonate adoptat, putem scrie asta
Evident, creșterile de coordonate ar trebui să aibă un semn plus sau minus, deoarece coordonatele punctului 2 pot fi mai mult sau mai puțin decât coordonatele punctului 1. Fără a acorda atenție semnalelor de creșteri de coordonate, scriem dintr-un triunghi drept
Luând în considerare schema din Fig. 6.3, scriem asta
și anume semnele incrementărilor coordonatelor sunt determinate de semnele funcțiilor sin și cos ale unghiurilor direcționale corespunzătoare. Apoi, pentru cazul general, formulele (7.1) iau forma
Exemplul 7.1. Problema geodezică directă.
Găsiți coordonatele punctului 2.
Problema geodezică inversă.
Formularea problemei geodezice inverse. din coordonatele cunoscute ale celor două puncte, găsiți poziția orizontală a liniei care leagă aceste puncte și unghiul de direcție.
Cu referire la Fig. 7.3: de la coordonatele cunoscute din punctele 1 și 2, găsiți distanța orizontală d12 și unghiul de direcție # 945; 12.
Problema geodezică inversă este folosită într-un număr mare de cazuri pentru determinarea unghiurilor de direcție ale direcțiilor inițiale, precum și pentru rezolvarea diferitelor probleme geometrice pe teren asociate cu construcția punctelor de proiectare a structurilor de inginerie pe teren (lucrări geodezice).
Se stabilește relația dintre semnele incrementelor coordonatelor și valorile unghiurilor de direcție (Tabelul 7.2).
Pentru a rezolva problema geodezică inversă, calculați incrementările coordonatelor
dacă se specifică sarcina de determinare a unghiului de direcție a direcției 1-2. Dacă, totuși, este necesar să se determine unghiul de direcție al direcției 2-1, atunci incrementările coordonatelor sunt determinate prin formule
Apoi calculați valoarea rumbei direcției specificate fără a lua în considerare semnele incrementărilor coordonatelor
și prin semne de incrementări ale coordonatelor, folosind tabelul. 7.2, selectați formula corespunzătoare pentru calcularea unghiului de direcție.
Semne de incrementări ale coordonatelor în funcție de amploarea unghiului de direcție
Unghiul de direcție al liniei poate fi astfel determinat pentru oricare dintre direcțiile sale și unghiul de direcție al direcției inverse, dacă este necesar, este determinat de formula unghiului de orientare inversă :.
Distanța orizontală de la triunghiul drept 123 se găsește prin formulele:
Valorile pozițiilor orizontale calculate prin formulele de mai sus ar trebui să coincidă practic în limitele erorilor de rotunjire.
Exemplul 7.2. Problema geodezică inversă.
Găsiți unghiul de direcție al direcției 1-2 și linia orizontală 1-2.
# 916; X2 = 9833,813 - 7273,856 = + 2559,957 m.
# 916; Y2 = 2165.041 - 5241.656 = -3076.615 m.
(Trimestrul al patrulea - NW) - a se vedea tabelul. 7.2.
Contrapartidele minore în valorile depunerii orizontale se datorează erorilor de calcul atunci când se rotunjește incrementările coordonatelor și unghiul de direcție.
Unghiul de direcție inversă.
Acest unghi poate fi obținut și prin calcularea directă prin creșterile corespunzătoare ale coordonatelor:
# 916; X1 = 7273,856 - 9833,813 = - 2559,957 m.
# 916; Y1 = 5241.656-2165.041 = + 3076.615 m.
(Al doilea trimestru SE) - a se vedea tabelul. 7.2.