Entropia alfabetului este cantitatea de informații pe simbol. Simbolurile unui alfabet echiprobabil poartă sarcina maximă de informații
Alfabetele de limbi naturale nu sunt la fel de probabile. De exemplu, frecvența relativă a apariției caracterelor personale rusești variază între 0,175 și 0,002.
Datorită proprietăților statistice ale alfabetului, încărcarea informației pe simbol este redusă cu
Redundanța alfabetului este reducerea încărcării de informații pe simbol datorită probabilității inegale și interdependenței apariției simbolurilor sale.
Redundanța informației, care caracterizează sub-încărcarea relativă a alfabetului, se calculează după cum urmează:
Codurile uniforme sunt caracterizate de o adâncime minimă a cuvintelor de cod, care este calculată prin formula
unde N este volumul alfabetului original A;
M este volumul alfabetului de cod B;
[logM N] denotă partea intregă a numărului logM N
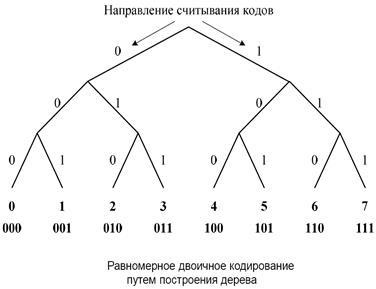
Să luăm în considerare aceste formule pentru cazul codării binare (adică pentru M = 2). Lățimea minimă de biți a unui cod uniform pentru un alfabet de 8 caractere este egală cu
rmin = log2 8 = 3 simboluri binare
Și pentru o alfabet de 9 litere
Codurile neuniforme se caracterizează prin lungimea medie a cuvântului de cod
li este lungimea cuvântului cod al celui de-al doilea caracter;
pi - probabilitatea apariției simbolului i;
N este volumul alfabetului original.
De exemplu, în cazul în alfabetul A = a, b, c, d, e> cu probabilitățile de apariție a caracterelor în mesajul (pa = 0,5; 0,2 = pb; pc = 0,1; pd = 0,15; pe = 0 , 05) binar cod codificate neuniform (a - 0; b - 10; c - 1110; d - 110; e - 1111), durata medie a cuvântului de cod pentru acest alfabet ar
Astfel, lungimea medie a unui cuvânt de cod este suma lungimilor tuturor cuvintelor de cod luate cu o greutate egală cu probabilitatea apariției simbolului codificat.
Numărul și cantitatea de informații


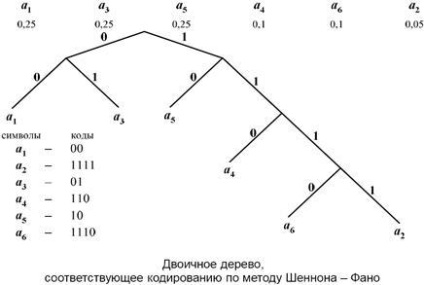
Metoda Shannon-Fano
Pasul 1. Aranjați simbolurile alfabetului original în ordinea de a nu crește probabilitățile lor. (Le scriem într-o linie).
Pasul 2. Fără a schimba ordinea simbolurilor, le împărțim în două grupe astfel încât probabilitatea totală a simbolurilor din grupuri să fie cât mai mult posibil.
Pasul 3. Atribuiți grupului din stânga "0" și grupul din dreapta "1" ca elemente ale codurilor lor.
Pasul 4. Uită-te la grupuri. Dacă numărul elementelor din grup este mai mare decât unul, mergeți la Pasul 2. Dacă există un element în grup, codul pentru acesta este completat.
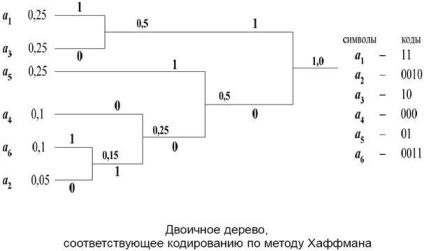
Pasul 1. Aranjați simbolurile alfabetului original în ordinea de a nu crește probabilitățile lor. (Le scriem într-o coloană).
Pasul 2. Combinați cele două simboluri cu cele mai mici probabilități. Este mai probabil ca simbolul să fie atribuit un "1", un simbol cu unul mai mic - "0" ca elemente ale codurilor lor.
Etapa 3. Considerăm unirea simbolurilor pentru un caracter cu o probabilitate egală cu suma probabilităților simbolurilor combinate.
Pasul 4. Reveniți la Pasul 2 până când toate simbolurile sunt combinate într-una cu o probabilitate egală cu una.