Orice sistem care presupune prezența unor stări discrete sau prezența unor noduri și tranziții între ele poate fi descris printr-un grafic. Conexiunile dintre nodurile (V) ale graficului sunt numite margini (E). Dacă nodurile graficului nu sunt numerotate, atunci marginile sunt ne-orientate. Într-un grafic cu noduri numerotate, marginile sunt orientate și sunt numite arce
(Figura 2).
O pereche de vârfuri poate fi îmbinată cu două sau mai multe muchii (arce), astfel de muchii (arce) sunt numite multiple. Vârfurile legate de o margine sunt numite adiacente. Dacă o margine începe și se termină la același vârf, atunci se numește o buclă.
Numărul de margini emanând de la vârful vi (bucla este numărată de două ori) se numește valență (gradul vârfului) și este notată cu: d (vi).
Dacă V și E sunt seturi finite, atunci graficul corespunzător acestora este declarat finit. Un grafic este numit degenerat. dacă nu are muchii.
Un grafic neorientat se spune simplu. dacă nu are bucle și orice pereche de vârfuri este conectată cu nu mai mult de o margine. Graficele sunt afișate în plan cu un set de puncte și linii sau vectori de conectare. Marginile pot fi afișate cu linii curbe, iar lungimea lor nu contează. Un grafic G se numește planar (plat). dacă poate fi afișat într-un plan fără a se intersecta cu fețele sale (figura 5). Se spune că un grafic este conectat. dacă pentru oricare dintre cele două vârfuri există o secvență de margini care le conectează (figura 3), adică graficul nu are fragmente izolate (vârfuri, muchii). Un grafic este numit complet. dacă există două vârfuri conectate doar printr-o margine (figura 4). Dacă graficul total are n noduri, numărul de margini va fi egal cu n (n-1) / 2. Tipurile speciale de grafice sunt arbori (figura 6), inele și liste, care nu sunt incluse în considerarea cursului nostru.
Un grafic al cărui vârfuri au același grad se numește un grafic obișnuit.
Adesea, pe un singur set de obiecte, sunt definite câteva relații binare diferite. Multigrafele servesc să reprezinte această situație. Multigrafele vor fi folosite pentru a reprezenta diagramele automatelor finite.
Marginea (arcul) și oricare dintre vârfurile sale sunt considerate a fi incidente. Noi spunem că (arc) muchie (u. V) se conectează nodurile u și v. În cazul în care nodul nu este incident nici o margine (arc), atunci se spune că este izolat (d (vi) = 0) dacă aparține numai o muchie (arc), numit apoi agățat (d (vi) = 1).
Prevederi de bază despre vârfurile graficului:
1. În graficul G suma gradelor de toate nodurile sale - un număr chiar egal cu de două ori numărul de muchii, deoarece fiecare parte margine din această sumă exact de două ori. Acest rezultat se numește lema handshaking: în cazul în care mai multe persoane au dat mâna, atunci numărul total de strângeri de mână este chiar necesară, pentru că în fiecare strângere de mână implică două mâini (cu fiecare mână este luată în calcul ori de câte ori ea a participat la strângere de mână).
2. Numărul de noduri ciudate ale oricărui grafic este egal.
3. În fiecare grafic cu n noduri, unde n ≥ 2, există cel puțin două noduri cu aceleași grade.
4. Dacă un grafic cu vârfuri n> 2 două vârfuri au același grad, în acest grafic există întotdeauna fie un nod de grad 0, sau un nod de gradul n - 1.
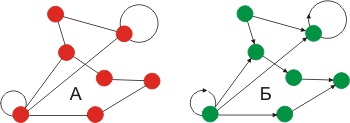
Două grafice G1 = (V1, E1) și G2 = (V2, E2) se consideră a fi izomorfe. Dacă există o corespondență unu-la-unu între vârfurile lor.
Algoritmul de recunoaștere a izomorfismului a două grafice G1 (X, E) și G2 (Y, E)
1. Dacă X ≠ Y, atunci graficele nu sunt izomorfe.
2. Se scriu toate elementele celor două grafuri prin definirea perechilor (xi, xj) și (yi, yj) pentru fiecare element, unde xi. yi este numărul de rezultate pentru fiecare vârf al ambelor grafice și xj. yj este numărul de vizite.
3. Pentru fiecare element x al graficului G1, căutăm un element y al graficului G2. că condiția este îndeplinită: numărul de rezultate x coincide cu numărul de rezultate y, iar numărul vizitelor x coincide cu numărul de vizite y. Conectăm elementele găsite x și y cu un arc, adică construim un grafic de corespondență. Dacă nu există corespondență, atunci graficele nu sunt izomorfe.
4. Scriem o permutare care duce graficul G1 la graficul G2.
Exemple de sarcini