Un grafic poate exista în diferite forme având același număr de vârfuri, muchii și aceeași conexiune de margine. Astfel de grafice se numesc grafice izomorfe. Rețineți că numim graficele din acest capitol în principal pentru a le referi la ele și a le recunoaște unul de celălalt.
grafice izomorfe
Două grafice G1 și G2 se consideră a fi izomorfe. dacă -
- Numărul lor de componente (vârfuri și muchii) este același.
- Legătura lor este păstrată.
NOTĂ - Pe scurt, din două grafice izomorfe, una este versiunea adaptată a celeilalte. Un grafic nemapat poate fi de asemenea considerat ca fiind izomorf la un grafic.
Gradul de secvență G1 și G2 este același.
Dacă vârfurile 1, V 2,. V k> formează un ciclu de lungime K în G 1, apoi vârfurile 1), F (V 2) ,. F (V k)> trebuie să formeze un ciclu de lungime K în G 2.
Toate condițiile de mai sus sunt necesare pentru ca graficele G 1 și G 2 să fie izomorfe, dar nu sunt suficiente. pentru a dovedi. că graficele sunt izomorfe.
(G 1 ≡ G 2) dacă și numai dacă. când (G 1 - ≡ G 2 -). unde G1 și G2 sunt grafice simple.
(G 1 ≡ G 2). dacă matricile G1 și G2 sunt aceleași.
(G 1 ≡ G 2) dacă și numai dacă. când subgrafurile corespunzătoare G 1 și G 2 (obținute prin eliminarea anumitor noduri în G 1 și imaginile lor din graficul G 2) sunt izomorfe.
Care dintre următoarele grafice sunt izomorfe?
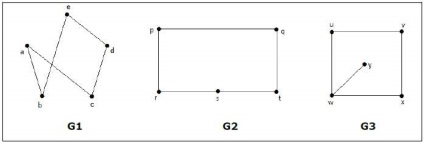
În graficul G 3, vârful "W" are doar gradul 3, în timp ce toate celelalte noduri ale graficului au gradul 2. Prin urmare. G 3. Nu este izomorf la G1 sau G2.
Luând suplimente de la G 1 și G 2, aveți -
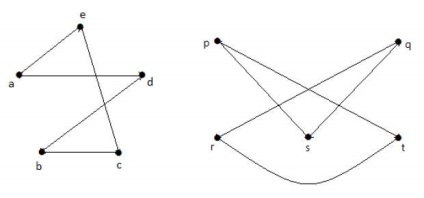
planuri grafice
Un grafic "G" se numește planar dacă poate fi desenat pe un plan sau o sferă, astfel încât nici două muchii nu se intersectează reciproc într-un punct, nu în vârf.
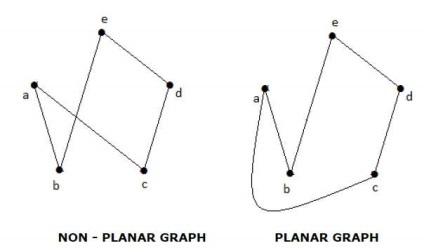
Fiecare grafic plat divide un avion în regiuni conectate, numite regiuni.
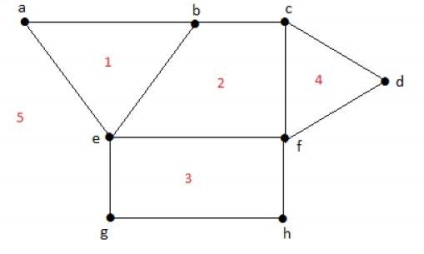
Gradul de regiune limitată este r = deg (r) = Numărul de margini care conțin regiunile r
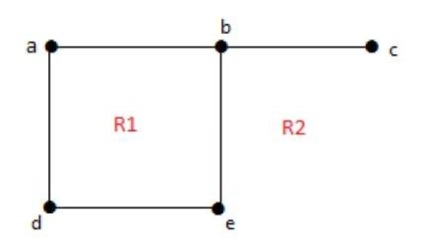
Gradul domeniului nelimitat este r = deg (r) = Numărul de margini care conțin regiunile r.
În graficele plate, următoarele proprietăți sunt bune -
1. Într-un grafic plat cu noduri "N", suma gradelor tuturor nodurilor
n Σ = 1 deg (V r) = 2 | E |
2. În concordanță cu suma gradelor din regiunile teoremei, în graful plat cu domenii "n", suma gradelor de regiuni -
n Σ = 1 deg (г г) = 2 | E |
Plecând de la teorema de mai sus, putem trage concluziile următoare:
Într-un grafic plat,
Dacă gradul fiecărei regiuni este K, atunci suma gradelor regiunilor
Dacă gradul fiecărei regiuni este cel puțin K (≥ K), atunci
Dacă gradul fiecărei regiuni nu este mai mare decât K (≤ K), atunci
Notă - Să presupunem. că toate regiunile au același grad.
3. Conform formula lui Euler pentru grafice plate,
Dacă graficul "G" este un plan conectat, atunci
| | V | + | R | = | E | + 2
Dacă un grafic plat cu componente "K", atunci
| | V | + | R | = | E | + (K + 1)
În cazul în care, | V | acesta este numărul de vârfuri, E | acest număr de muchii și R | acesta este numărul de regiuni.
4. inegalitatea de vârf a vârfurilor
Dacă "G" este un graf plat conectat cu un grad de fiecare regiune de cel puțin "K", atunci,
Știți | V | și plus; | | R | = | E | și plus; 2
K (| E | - | V | plus; 2) ≤ 2 | E |
(K - 2) E | ≤ K (| V | - 2)
5. Dacă "G" este un grafic plat simplu conectat, atunci
Există cel puțin un vertex V ∈ G astfel încât gradul (V) ≤ 5
6. Dacă "G" este un grafic planar conectat simplu (cel puțin 2 margini) și fără triunghiuri, atunci
7. Teorema lui Kuratowski
Graficul "G" nu este plat dacă și numai dacă. când 'G' are un subgraf homeomorphic la K 5 sau K 3,3.
homomorfism
Două grafice G1 și G2 se consideră a fi Homomorfe dacă fiecare dintre aceste grafice poate fi obținut din același grafic "G" prin împărțirea unor margini ale lui G cu un număr mare de vârfuri. Aruncați o privire la următorul exemplu -
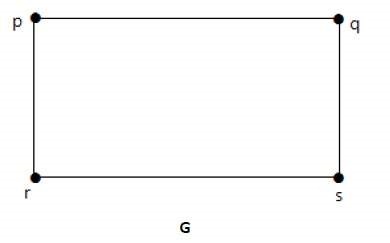
Împărțiți marginea "RS" în două margini, adăugând un vertex.
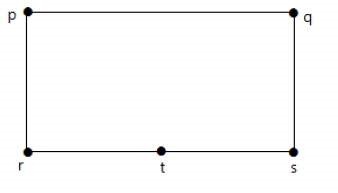
Graficele prezentate mai jos sunt homomorfice la primul grafic.
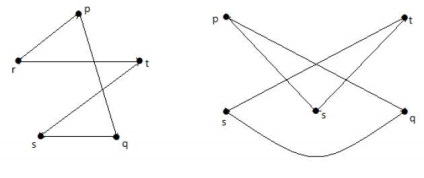
Dacă G 1 este izomorf la G 2, atunci G este homeomorf la G 2. Dar conversația nu trebuie neapărat să fie adevărată.
Orice grafic cu 4 sau mai multe noduri este plat.
Orice grafic cu 8 sau mai puțin marginile este plat.
Un grafic complet K n este plat dacă și numai dacă. atunci când n ≤ 4.
Un grafic complet bipartit K m, n este plat dacă și numai dacă. atunci când m ≤ 2 sau n ≤ 2.
Un simplu grafic neplanar cu un număr minim de noduri este graficul complet K 5.
Un grafic simplu nonplanar cu un număr minim de margini K 3, 3.
Graficul cu multe fațete
Un graf plat simplu conectat este numit graf poliedteral dacă gradul fiecărui vârf este ≥ 3, adică gradul (V) ≥ 3 ∀ V ∈ G.