Există modalități diferite de a ilustra planul phi-gur-ului, situat în spațiu. Aici ar trebui să menționăm o metodă bazată pe design paralel.
Alegem un avion # 963; și numiți planul imaginii. Apoi vom lua un vector nenul. nu paralel cu planul # 963; Direcția acestui vector va fi denumită direcția de proiectare. Fie F o figura arbitrară (plană sau spațială) situată în spațiu și F0 este proiecția paralelă a acestei figuri pe plan # 963; Figura F 'se numește originalul. și F0 este proiecția originalului. Orice figură F în avion # 963; similar cu figura F0. se numește imaginea figurii F '(Figura 2.1). Imaginea figurii astfel construite corespunde percepției sale vizuale atunci când este privită dintr-un punct aflat departe de figură.
În alegerea imaginilor pentru un anumit desen (cifrele de imagine nu este numai proiecția sa, dar orice figură, această proiecție) poate fi explicată prin următorul fapt. De obicei, planul imaginii este planul hârtiei și proiecția originalului nu sunt plasate întotdeauna pe foaia, și dacă sunt plasate, nu va fi întotdeauna situat convenabil. În aceste cazuri, în avion # 963; proiecția F0 a originalului F 'este supusă unui plan # 963; similaritatea transformării astfel încât imaginea F a figurii F0 să aibă un aranjament convenabil și dimensiuni convenabile.
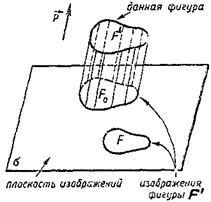
Astfel, imaginea unei forme depinde de alegerea planului imaginii # 963; direcția de proiectare și similitudinea selectată a planului # 963; De obicei, este luată o figură, care este cea mai vizuală și convenabilă pentru realizarea unor construcții suplimentare pe ea.
Construcția de imagini ale figurilor folosind design paralel se bazează pe proprietățile designului paralel și ale mapărilor afine. Să luăm în considerare exemplele de construire a imaginilor de planuri studiate în cursul școlii de geometrie. Procedând astfel, vom presupune că planurile originale și ale imaginii se intersectează și că direcția de proiectare nu este paralelă cu niciuna dintre aceste planuri. Pentru a realiza construcția, este necesar să cunoaștem teorema imaginilor cu figuri plane.
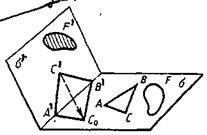
Teorema. Să presupunem că figurile F 'și F se găsesc pe planurile intersectate # 963; și # 963; Figura F poate servi drept imagine a figurii F 'dacă și numai dacă figurile F' și F sunt echivalente afine.
1) Lăsați figura F a planului # 963; este o imagine a figurii F 'a planului # 963; ". Dovedim că F 'și F sunt echivalente afine. Luați în considerare proiecția F0 din F '. Deoarece proiecția paralelă este o hartă afinică, F 'este afine-echivalentă cu F0. Pe de altă parte, F0 și F sunt similare, deci sunt echivalente afine. Astfel, figurile F 'și F sunt echivalente afine.
2) Să presupunem acum că figura F 'a planului # 963; este echivalenta cu figura F a planului # 963; Să demonstrăm că figura F poate fi privită ca o imagine a figurii F '. Deoarece cifrele F 'și F sunt echivalente afine, există o mapare afină f. # 963; → # 963, astfel încât F = f (F '). Alegem cadrul R '= (A', B ', C') al planului # 963; astfel încât punctele A 'și B' să fie situate pe linia de intersecție a planurilor # 963; și , Considerăm imaginea R = (A, B, C) a acestui cadru sub harta f (Figura 2.2).
În avion # 963; vom construi punctul Co, astfel încât # 8710; A'B'C0
# 8710; ABC. Proiecție paralelă f. # 963; → # 963; în direcția vectorului, cadrul R 'se transformă în cadrul R0 = (A', B ', C0). Luați în considerare similitudinea lui f2. # 963; → # 963; care transferă cadrul R0 la cadrul R. Evident, f2f1. # 963; → # 963; este o mapare afină care transferă cadrul R 'către cadrul R. Prin urmare, prin teorema 1, coincide cu harta f. Astfel, F = f2f1 (F). Dar F0 = f1 (F ') este proiecția paralelă a figurii F' pe plan Deci F = f2 (F0) este imaginea figurii F '.
Folosind teorema precedentă, să luăm în considerare construirea de imagini ale anumitor poligoane. Prin teorema imaginilor cu figuri plane, imaginea unui n-gong este o figură affine-echivalentă cu originalul, adică n -gon. Prin urmare, imaginea triunghiului este un triunghi, un patrulater - patrulater, pentagon - pentagon etc. Cu toate acestea, după cum rezultă din aceeași teorema fără nici un avion-gon n .. # 963; poate servi ca o reprezentare a unui anumit n-unghi al planului # 963; ". Luați în considerare această problemă mai detaliat pentru n = 3 și n = 4.
a) Triunghi. Orice plan triunghiular ABC # 963; poate servi drept imagine a planului triunghiului A'B'C # 963; dacă avionul # 963; și # 963; se intersectează. De fapt, prin Teorema 1 există o hartă afină f. # 963; → # 963, pe care cadranul (A ', B', C ') ajunge la cadru (AVC), prin urmare triunghiurile A'B'C' și ABC sunt echivalente afine. Prin teorema anterioară, triunghiul ABC poate servi ca imagine a triunghiului A'B'C '.
b) Quadrilateral. Prin teorema imaginilor plane, orice quadrilater al avionului # 963 ;, echivalentul afine cu acest quadrangle F 'al avionului # 963; poate servi drept imagine în cazul avionului # 963; și # 963; se intersectează. Din Teorema 2 concluzionăm că nu fiecare patrulater al avionului # 963; poate servi ca imagine a quadranglei F '. Pentru a construi imaginea ABCD a unui quadrangle dat A'B'C'D ca vârfuri A. B și C, putem alege trei puncte arbitrare care nu se află pe o linie. În acest caz, imaginea D a celui de-al patrulea punct D 'este determinată în mod unic de condițiile respective
c) Trapez. Figura, un trapez echivalent afine, este un trapez, astfel încât trapezoidul este un trapez. Condițiile (1) în cazul unui trapez înseamnă că raportul dintre bazele originalului este egal cu raportul dintre bazele imaginii. Astfel, planul F-trapezoid # 963; Este o vedere trapezului F „numai în cazul în care raportul dintre bazele trapez F“ este egal cu raportul dintre trapezului de bază F“.
d) paraleleogramele (incluzând un romb, un dreptunghi, un pătrat) sunt reprezentate ca o paralelogramă. Deoarece orice două paralelograme sunt echivalente afine (Teorema 2), orice paralelogram al planului imaginii este o imagine a acestui paralelogram - originalul. În particular, orice paralelogram al planului # 963; este imaginea pătratului planului # 963; .
e) n -Shadow. unde n> 4. Din prezentarea precedentă rezultă că pentru a construi o imagine a unui n -gon dat pentru n> 4, trei noduri ale imaginii pot fi alese în mod arbitrar, iar nodurile rămase sunt construite.
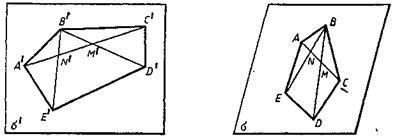
Figura 2.3 prezintă imaginea pentagonului A'B'C'D'E '. Vinetele A și B sunt alese arbitrar, iar vârfurile D și E se găsesc prin construcție. D. vertex de exemplu, construite folosind condiții (B'D 'M ') = (BD. M), (A'S'. M') = (AC. M). În figura 11, este construită o imagine a hexagonului obișnuit A'B'C'D'E'F cu centrul în punctul O '. În acest caz, este mai convenabil să ia punct arbitrar A. Un punct D VO construi ca un punct simetric la punctul A în raport cu punctul O. Pentru a construi punctul C construct în soare direct și condiții DC soare || AB. DC || BO. Punctele E și F sunt construite ca puncte simetrice față de punctele B și C în raport cu punctul 0.
f) Cercul. Construcția imaginii cercului se bazează pe următoarea afirmație.
Lema. În orice hartă afinică o elipsă (în special, un cerc) intră într-o elipsă.
Din această lemă, luând în considerare teorema anterioară, concluzionăm că imaginea unui cerc dat este o elipsă. Imaginea centrului cercului este centrul elipsei, iar imaginea diametrelor reciproce perpendiculare este diametrele conjugate ale elipsei.