Dezvoltarea reprezentărilor spațiale este unul dintre cele mai importante obiective ale educației școlare. Experiența arată că elevii clasei a 5-a au deja suficiente reprezentări spațiale inițiale asociate experienței lor de viață și obiectelor din realitatea din jur. Copiii "trăiesc" în lumea spațială, consideră planul o figură geometrică, citesc desene bine, mulți sunt capabili să reprezinte figuri spațiale, să fanteze, deși nu pot funcționa cu imagini mentale. În clasele 5-6 există, de asemenea, oportunități de formare a reprezentărilor spațiale inițiale. Cu toate acestea, până la sfârșitul studiului de planimetrie, elevii din clasa a IX-a sunt deja ferm atașați de avion, nu o consideră o figură geometrică, ci un loc pe care se află figurile plate.
Acest lucru sugerează că gândirea spațială a elevilor din clasa a IX-a este suprimată, deoarece atenția copiilor este întârziată artificial în planimetrie. În acest sens, este recomandabil să se studieze întrebările planimetrice cu ajutorul materialelor stereometrice sau, în paralel cu cursul tradițional de planimetrie, să se desfășoare clase elective care extind foarte mult gama de figuri studiate și proprietățile lor.
Lecția de geometrie propusă se poate face în clasele 7-9.
1. Dezvoltarea gândirii spațiale.
3. Învață să reprezinți în mod corect forme spațiale.
4. Educarea culturii grafice a studenților.
Echipament:- Proiector multimedia, ecran sau tablă interactivă, calculator.
- Prezentarea lecției.
- Modele de piramide, prisme, cilindri, conuri, inclusiv cabluri.
- Cerc de cerneală, pictat în culori strălucitoare.
- Pahare pe fiecare masă.
- Soluție de mangan în vase mari cilindrice și conice.
1. Revizuiți și analizați desenul final.
2. Luați în considerare cele mai simple corpuri geometrice, deduceți regulile imaginii lor, trageți aceste corpuri.
3. Aplicați-vă cunoștințele pentru a construi desene.
4. Să se familiarizeze cu conceptul de secțiune.
1. Moment organizatoric.
2. Muncă orală.
Această parte a lecției vizează lărgirea viziunilor stereometrice generale și dezvoltarea gândirii spațiale a studenților. Este important să folosiți figurile modelului, desenele și imaginile mintale. Este trecerea de la imaginile spațiale ale obiectelor reale la imaginile grafice condiționate, de la imagini tridimensionale la imagini bidimensionale și în spate, adică transcodarea constantă a imaginilor este o gândire spațială.
- Ce este un avion? Dați exemple ale avionului în studiu.
- Câte avioane există în spațiu?
Copiii trebuie să învețe că planul este aceeași figură geometrică ca și poligoanele deja cunoscute, cercul etc. și că avioanele situate în poziții diferite, există un număr infinit. Puteți modela un avion utilizând un manual sau un notebook, remarcând încă o dată că aceasta este doar o parte a avionului, avionul în sine este infinit.
- Ce fel de figura este descrisă <рисунок1>? (diapozitivul 3).
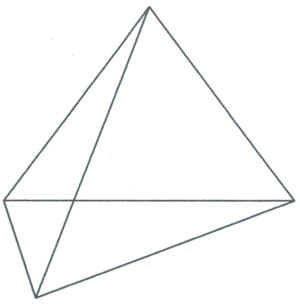
Desenul ar trebui să fie exact așa, fără liniile punctate. Copiii ar trebui să vadă nu doar cvadrangul, ci și piramida cvadrangulară "de sus", piramida triunghiulară "transparentă".
- Care piramidă este descrisă? (quadrangular, triunghiular)
- Ce cifră se află la baza ei?
Copiii ar trebui să vadă cifrele obișnuite "plate" în voluminoase.
- Ce forme geometrice știi?
Este necesar ca studenții să cheme nu numai figuri plate, ci și ele tridimensionale.
- Denumiți corpurile geometrice.
Profesorul arată modelul, îi sună copiii.
3. Imaginea figurilor.
- Desenează figuri plate - triunghiuri, quadrangles etc. - suntem capabili. Și cum au desenat figuri tridimensionale?
- Ce este designul (explicația profesorului).
Arătați în exemplul unei umbre exprimate pe ecran printr-un model cadru al unei piramide triunghiulare. Imaginea umbrei este transferată la bord.
- De ce este această imagine incomodă? (se pare că segmentele se intersectează, deși de fapt - nu, nu este clar ce este prezentat)
- Regula: Linii care sunt în figura obișnuită <рисунок2> (diapozitivul 4) nu sunt vizibile, tragem cu o linie întreruptă (diapozitivul 5).
Dezasamblați modelul, ce linii sunt transmise neschimbate și care sunt distorsionate.
- Proprietățile proiecției (profesorul însuși numește aceste proprietăți, sau dacă există timp, copiii le pot scoate):
1. Se păstrează paralelismul liniilor drepte.
2. Proiecția mijlocului segmentului este mijlocul proiecției sale (diapozitivul 6).
- Cum de a desena piramida quadrangulară dreapta?
a) baza (în ce figură merge pătratul?);
b) diagonalele bazei;
c) înălțime (prin punctul de intersecție al diagonalelor);
d) coaste laterale.
Un desen pentru semn ("piramida quadrangulară").
- Cât de corect să trageți piramida dreptunghiulară potrivită?
Studentul este chemat la bord.
Baza se transformă într-un triunghi non-isoscel. Copiii trebuie să tragă o concluzie, unde se află baza înălțimii: înălțimea pe care o trecem prin punctul de intersecție al medianilor. Dezasamblați de ce construim medii - de proprietatea numărului 2 de proiecție. Un desen pentru semnarea "piramidei triunghiulare".
- Cum de a desena un cilindru drept circular?
Ce e în partea de jos a cilindrului? Ce va arata baza pe desen? Un experiment este realizat cu un cerc din carton: în primul rând, profesorul deține cercul în planul vertical, apoi se rotește în jurul diametrului orizontal <рисунок3>. Pentru ce este destinat cercul? (în elipse).
Profesorul se apropie de copii: semiaxisul mic este de 2 ori mai mic decât cel mare. Desen pentru a semna "cilindrul".
- Cum de a construi un con?
Studentul este chemat la bord.
4. Construcția secțiunilor.
- Ce este o secțiune? (explicația profesorului).
- Ce se poate întâmpla când o minge este tăiată de un avion? (exemplu: pepene verde este tăiat în două părți).
Această concluzie trebuie făcută de studenți fără desen și model.
- Ce se poate întâmpla în secțiunea cilindrului?
Experiența cu permanganatul de potasiu în paharul de laborator. Se toarnă fiecare student în paharul de laborator o soluție. Avem un cerc. Îndoiam paharul. Obțineți o elipsă sau o parte din ea <рисунок4>. În notebook-urile de pe cele două imagini ale cilindrului desenați diferite tipuri de secțiuni (diapozitivul 7).
- Ce se poate întâmpla în secțiunea conului? (experiența cu permanganatul de potasiu în conul de oală).
Acordați atenție: în ciuda faptului că partea superioară a conului are o rază mai mică de curbură, o elipsă cu aceeași rază de curbură în părțile superioare și inferioare <рисунок5>. Nu este nevoie să construiți un desen în notebook-uri (diapozitivul 8).
- Ce se poate întâmpla în secțiunea transversală a piramidei? (poligoane).
Profesorul prezintă desenele finalizate <рисунок6> (diapozitivul 9).
5. Muncă independentă.
Despre opțiunile.- Varianta I. Construiește un paralelipiped.
- Opțiunea II. Construiți o prismă triunghiulară într-o poziție verticală.
- Opțiunea III. Construiți o prismă triunghiulară într-o poziție orizontală. Modele de cadre introduse pe tabelul demonstrativ.
6. Rezumați lecția.