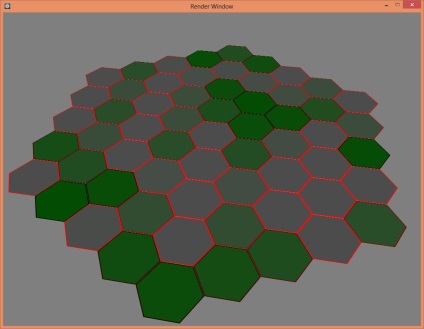
Bună ziua. Recent am întâlnit problema generării unei grile hexagonale din centru. Există metode de generare a liniilor. Sunt potrivite pentru orice. Și nu am găsit o astfel de metodă. Poate m-am uitat rău, cine știe. La forum mi-au fost oferite trei curbe:
1. Curături (cea mai proastă opțiune).
2. Linia de generare pe linie și aruncarea inutilă. În principiu, decizia cea mai corectă, dar, din păcate, trebuie să o fac din centru. Apoi, va fi convenabil să adăugați celulele necesare.
3. Coordonate înclinate. Acesta este un megaș complex, la care puteți ucide un nor de timp. Nu puteam să o înving.
Și acum, hai să mergem la algoritmul nostru.
Esența degetelor
Trebuie să obținem o structură celulară pentru asta.
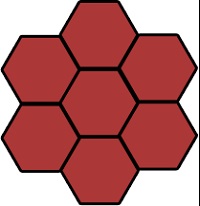
Primul pas este generarea primului hexadecimal central.
Dacă privitorul nostru este suficient de perspicant, el va observa că celulele adiacente pe laturi formează axele matricei.
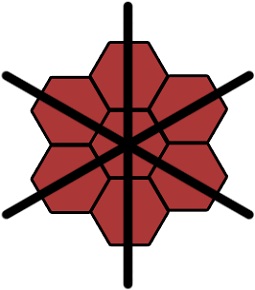
Cu prima serie de probleme nu apare, dacă știți raza și unghiul, atunci toate hexagoanele vor cădea așa cum ar trebui. Problemele sunt legate de cea de-a doua serie. Unele celule nu vor mint acolo unde este necesar. Iar motivul este următorul. În structura noastră există o periodicitate. Dar nu este circular, ci hexagonal. Doar în primul rând converg.
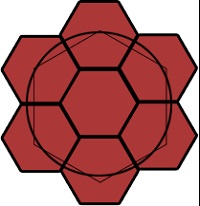
Figura arată că centrele hexagonilor se află atât pe cerc, cât și pe hexagonul matricei. Cu toate acestea, în al doilea rând, problema este clar vizibilă.
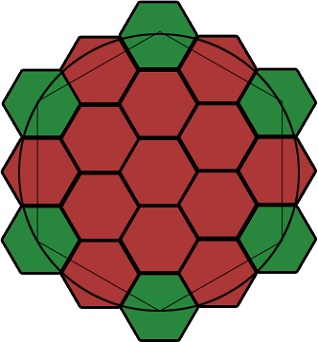
Se poate observa că numai hexagoanele axiale (cele verzi) se află pe un cerc. Centrele celorlalți sunt deplasate spre centru și se află pe hexagonul matricei. Prin urmare, o astfel de rețea nu poate fi specificată prin simetrie radială.
De aici urmează următoarea soluție.
Construim mai întâi numai hexagoane axiale.
Apoi vom calcula vectorii. Figura arată direcția vectorilor. Poate fi invers.
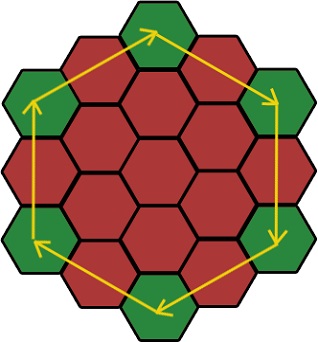
Dar nu avem nevoie de acest vector. Mai exact nu el însuși, ci partea lui.
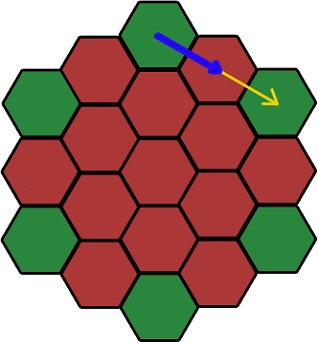
Avem nevoie de un vector albastru. Această deplasare, care este adăugată hexagonului axial pentru obținerea coordonatelor exacte. Vectorul galben este împărțit la numărul de piese egale cu numărul de hexagoane dintre hexagonii axiali + 1 (sau numărul de strat).
După aceasta, puteți genera matrici arbitrar mari din centru.
Și acum voi aduce codul, această rușine. Am programat pe Xors3D, dar cred că cine are nevoie de el, el va înțelege cum funcționează acest lucru (mai ales codul este simplu și esența explicată mai sus). Avem nevoie de o singură funcție - funcția de a crea o celulă.
Iată codul ei.
; Calculul vectorilor
Dacă ordinați> 0 Apoi - calculați vectorul dacă seria nu este zero (în cazul în care hexa centrală este)
Vector (i, 0) = ((CellRadius * Sin (Angle + 60) * Comanda-CellRadius * Sin (Angle) * Ordinul)) / (comandă) - 0 = X, coordona primul vector
Vector (i, 1) = ((CellRadius * Cos (Angle + 60) * Comanda-CellRadius * Cos (Angle) * Ordinul)) / (comandă) - 1 = Z, vectorul doua coordonate
Sfârșit Dacă
următor
Ce avem la ieșire:
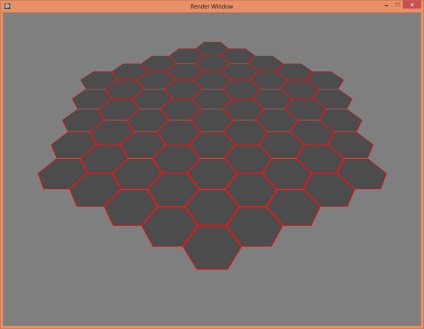
Upgrade 1.0 - Rotiți în orice unghi al matricei
Pot exista situații în care grila noastră hexagonală ar trebui să fie undeva să se alăture în unghiul drept. M-am gândit la asta și am modernizat funcția - acum puteți roti întreaga matrice într-un unghi arbitrar!
Deci, codul este:
Diferențe importante:
Funcția CreateCell (X #, Z #, Order%, AddAngle%) - a apărut un nou argument, acesta este un unghi arbitrar - AddAngle.
Unghi # = 360 / Limit * i + AddAngle - adăugați un decalaj pentru a calcula unghiurile și vectorii.
xRotateEntity Cell \ Sprite, 90, -AddAngle, 0 - rotiți sprite-ul în jurul axei verticale în direcția opusă.
Ce avem la ieșire:
17 de grade.
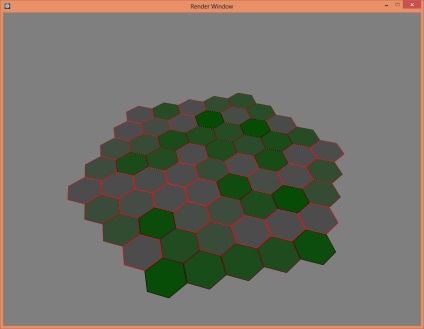
30 de grade.
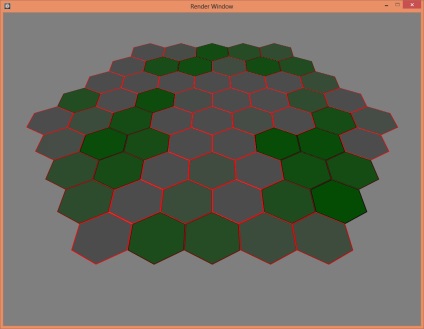
10 grade.