Lăsați corpul să fie limitat de avioane și. Fie ca fiecare secțiune a corpului să fie o figură cvadratabilă. iar zona sa este o funcție continuă pe segment. Apoi corpul va fi cubabil, iar volumul său este calculat prin formula.
Considerăm o împărțire a unui interval printr-o colecție finită de puncte
. Apoi. unde volumul părții corpului închis între planuri și. În fiecare segment parțial al partiției alegem un punct. Secțiunea corpului de către plan este o figură cvadratabilă. Zona este o funcție continuă, prin urmare, dacă segmentul este suficient de mic, atunci acesta se schimbă puțin, așa că putem presupune acest lucru. Apoi volumul este aproximativ egal cu volumul prismei cu suprafața de bază și înălțimea. Având în vedere formula volumului de prisme, obținem. Apoi, volumul întregului corp este aproximativ egal. Deoarece în partea dreaptă a acestei egalități există o sumă integrală Riemann pentru o funcție pe un interval. atunci pentru finețea partiționării tinzând la zero, obținem formula.
Un exemplu. Găsiți volumul elipsoidului.
Soluția. Scrieți ecuația elipsoidului :.
Gasim sectiunea transversala a elipsoidului cu avionul:
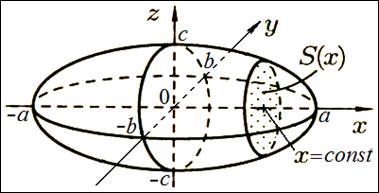
În secțiunea elipsoidului, planul este o elipsă cu semiaxe
și. Zona acestei elipse este
. Substituind în formula care calculează volumul corpului prin zona secțiunilor transversale, obținem
În cazul particular în care toate semiaxele elipsoidului sunt egale și egale. obținem formula pentru volumul unei sfere.