Secțiunea unei sfere de către un avion
TEOREM 20.3. Fiecare secțiune a unei sfere de către un avion este un cerc. Centrul acestui cerc este baza perpendicularului căzut de la centrul sferei pe planul de tăiere.
Dovada. Fie ca planul secant și D să fie centrul sferei (Figura 453). Punem perpendicularul din centrul sferei în plan și indicăm D 'baza acestei perpendiculare.
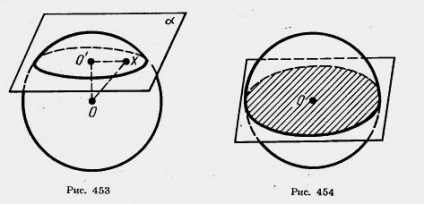
Fie X un punct arbitrar al mingii care aparține avionului. Prin Teorema lui Pitagora 2 = 0X 00 „2+ O'x 2. Deoarece OX nu este mai mare decât raza R a balonului, atunci. t. e., orice plan în secțiune a punctului bilei este din punctul O „la o distanță nu mai mare. în consecință, aparține unui disc cu centru O 'și rază.
În schimb, orice punct X din acest cerc aparține mingii. Aceasta înseamnă că secțiunea mingii de către avion este un disc cu centru în punctul O '. Teorema este dovedită.
Planul care trece prin centrul sferei se numește planul diametral. Secțiunea transversală a unei sfere printr-un plan diametral se numește un cerc mare (Figura 454), iar secțiunea sferei este un cerc mare.
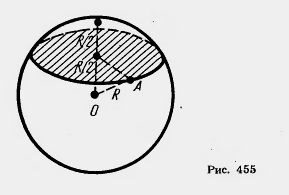
Problema (30). Un plan perpendicular pe acesta este tras prin mijlocul razei sferei. Cum se referă suprafața secțiunii rezultate la zona unui cerc mare?
Soluția. Dacă raza mingii R (Figura 455), atunci va fi raza cercului din secțiune
.
Raportul ariei acestui cerc cu aria cercului mare este
A. Pogorelov, Geometria pentru gradele 7-11, Manual pentru instituțiile de învățământ
Dacă aveți corecții sau sugestii pentru această lecție, scrieți-ne.
Dacă doriți să vedeți alte ajustări și dorințe pentru lecții, consultați aici - Forumul educațional.