Înlocuind coordonatele punctului C (6; 5) în funcția obiectiv, obținem soluția problemei:
.

1.5. Seturi convexe
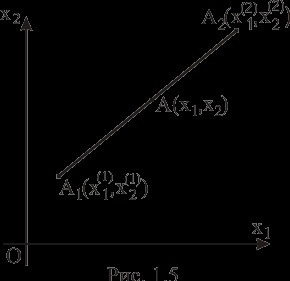
collinear, atunci, unde sau
, , .
Având în vedere că în (5.12) coordonatele punctului A sunt sumele acelorași coordonate ale punctelor u, înmulțite cu, respectiv, obținem în final
Definiție 1.10 Un punct A este o combinație liniară convexă de puncte și dacă sunt îndeplinite condițiile (1.13) pentru acesta.
Definiția 1.11 În cazul general, un punct A este o combinație liniară convexă de puncte dacă este cazul
Definiție 1.12 Un set se spune a fi convex dacă conține o combinație liniară convexă a oricărui punct al acestuia.
Din punct de vedere geometric, aceasta înseamnă că, dacă două puncte aparțin unui set, segmentul care leagă aceste puncte aparține acestui set.
Exemple de seturi convexe sunt un segment, o jumătate de plan, un poligon, un cerc, o jumătate de spațiu, un cub,
Definiția 1.13 Un punct al unui set este considerat a fi limită dacă orice vecinătate dintr-un punct dat conține atât puncte care aparțin setului, cât și puncte care nu aparțin setului.
Definiție 1.14 Se spune că un set este închis dacă conține toate punctele sale limită.
Definiție 1.15 Un set se consideră a fi limitat dacă este astfel încât o minge de rază Rc cu centrul în orice punct al unui set dat conține complet acest set.
Definiție 1.16 Un punct de colț al unui set convex este un punct care nu este o combinație liniară convexă a oricărui punct distinct al acestui set.
Un set poate avea orice număr de puncte de colț: unul (Figura 1.6, a), două (Figura 1.6, b), trei (Figura 1.6, c) etc. și un număr infinit de puncte de colț (figura 1.6, d).
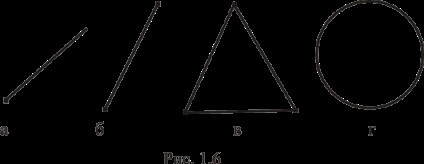
Este posibil ca setul să nu aibă puncte de colț, de exemplu o linie dreaptă, o jumătate de plan, etc.
Definiție 1.17 Un polyhedron este un set convex, închis, delimitat care are un număr finit de puncte de colț.
1.6. Proprietățile soluțiilor la probleme
Teoremele 1.2-1.5 de mai jos definesc proprietățile unui set de soluții admisibile și o funcție obiectivă asupra setului de planuri admisibile.
TEOREM 1.2. Setul de planuri admisibile ale problemei (1.15), (1.16) este un set convex.
THEOREM 1.3. Funcția obiectivă a problemei (1.15), (1.16) atinge un extremum la punctul de colț al setului de planuri admisibile. Dacă funcția obiectiv atinge un extremum la mai multe puncte de colț, atunci ajunge la un extremum în orice combinație liniară convexă a acestor puncte.
,..., sunt vectori de condiție, atunci sistemul de constrângeri (1.16) din notația vectorului are forma:
TEOREM 1.4. Dacă sistemul de vectori de condiție este liniar independent și este astfel de
,
unde, atunci este punctul unghiular al setului de soluții ale sistemului de constrângere.
Teorema 1.5. Dacă este punctul unghiular al setului de soluții ale sistemului de constrângere, atunci vectorii condiției care corespund coordonatelor pozitive sunt independenți liniar.
Definiție 1.18.Planul de suport (soluție) al problemei de programare liniară este un plan admisibil pentru care vectorii de condiție corespunzători coordonatelor sale pozitive sunt liniar independenți.
Din teoremele 1.4 și 1.5 rezultă că punctele de colț ale setului de soluții ale sistemului de constrângeri sunt planuri de sprijin.
Definiția 1.19.În cazul în care planul de sprijin m nu este zero, se consideră că planul este nondegenerat dacă m este degenerat.
Definiția 1.20 Baza planului de suport este baza sistemului de vectori condiționali, care include vectori corespunzători coordonatelor nonzero ale planului suport.
Rezultă din teoremele 1.2-1.5 de mai sus că soluția optimă a problemei de programare liniară (1.15), (1.16) trebuie căutată printre punctele de colț ale setului de planuri admisibile. În acest sens, apar următoarele întrebări:
- cum să găsiți un plan inițial?
- cum să treceți de la planul inițial de susținere la cel nou (de la un punct de colț al soluției polyedron la celălalt)?
- Cum se evaluează schimbarea funcției obiective atunci când se trece de la un plan de suport la altul?
- cum se determină sfârșitul procesului de enumerare a punctelor unghiulare: fie pentru că se găsește o soluție optimă, fie pentru că nu există o astfel de soluție, adică Care sunt condițiile pentru optimalitatea planului de sprijin?
Răspunsurile la aceste întrebări sunt prezentate în secțiunea următoare 1.7.
1.7. Construirea planurilor de referință
Procesul de construire a planului inițial de susținere, trecerea ulterioară la un nou plan de sprijin (mai bun), va fi luată în considerare utilizând exemplul unei probleme LP cu cinci variabile și trei ecuații într-un sistem de constrângeri. În prima etapă, vom presupune că fiecare variabilă din sistemul de constrângeri conține doar o variabilă cu un coeficient.
1.7.1 Elaborarea unui plan inițial de referință
Vom analiza problema
Sistemul de ecuații (1.19) conține trei vectori unici
, , .
Acestea formează o bază în sistemul de vectori ,,,,.
În conformitate cu schema generală de rezolvare a SLAU nedeterminată, declarăm variabilele ,, bază, și - liber și presupunem. Apoi SLAU (1.19) are următoarea formă:
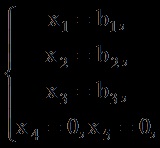
iar soluția SLAU este un vector. Planul rezultat va fi un plan admisibil, deoarece coordonatele sale pozitive corespund vectorilor independenți liniar ,,, și
.
Planul de suport inițial construit oferă valoarea funcției țintă
.
Să luăm în considerare un exemplu concret
Exemplul 1.4. Rezolva problema LP.
1. Selectarea planului inițial de referință
Setul de planuri admisibile ale problemei este determinat de un sistem de ecuații liniare (1.21). Acest sistem poate fi rescris în formă vectorică