2. Calcularea valorilor funcției z ij = f (x i; y j) la toate nodurile rețelei.
3. Un apel la funcția de a construi grafice tridimensionale.
5.1 Funcțiile plot3d și plot3d1
În Scilab, suprafața poate fi construită folosind funcțiile plot3d sau plot3d1. Diferența lor este că plot3d construiește o suprafață și un golf-
o singură culoare, și compară suprafața, fiecare dintre ele având o culoare, în funcție de valoarea funcției din fiecare nod corespunzător al rețelei (a se vedea Figura 5.11).
Apelul la funcții este după cum urmează:
5.1. Funcțiile plot3d și plot3d1
aici x este un vector de coloană al valorilor abscisei;
y vector-coloană a valorilor ordinelor;
z este matricea valorilor funcției;
theta, alpha sunt numere reale care determină în grade coordonatele sferice ale unghiului de vedere al graficului. Pur și simplu, acesta este unghiul la care observatorul vede suprafața afișată;
piciorul semn axele de coordonate ale simbolurilor grafice separate de semnul @. De exemplu, "X @ Y @ Z".
array de pavilion format din trei parametri întregi: [mode, type, box]. aici
Modul stabilește culoarea suprafeței (a se vedea tabelul 5.1). Valoarea implicită este de 2 culori albastre, se afișează grila rectangulară.
Tabelul 5.1. Valorile pentru parametrul modului
> 0 suprafața are culoarea ¾mode¿, este trasă o rețea dreptunghiulară
0 afișează o rețea dreptunghiulară, fără umplere (culoare albă)
<0 поверхность имеет цвет ¾mode¿, отсутствует прямоугольная сетка
tip vă permite să controlați scala graficului (vezi Tabelul 5.2), în mod implicit are valoarea 2;
(vezi Tabelul 5.3). Valoarea implicită este 4.
ebox definește limitele zonei la care va fi transmisă suprafața, ca vector [xmin, xmax, ymin, ymax, zmin, zmax]. Acest parametru poate fi utilizat numai pentru valoarea parametrului de tip = 1.
keyn = secvența de valori a valorilor proprietăților graficului key1 = value1, key2 = value2. keyn = valuen,
cum ar fi grosimea liniei, culoarea acesteia, culoarea de umplere a fundalului ferestrei grafice, prezența unui marker etc. (a se vedea punctul 4.6).
Astfel, funcțiile plot3d (plot3d1) ca parametri trebuie să fie transferate într-o rețea dreptunghiulară și o matrice de valori în nodurile rețelei.
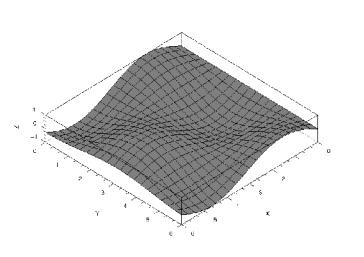
Construiți un grafic al funcției Z = sin (t) cos (t).
Creați o serie de valori pentru argumentul t. Calculăm valorile funcției și le scriem în matricea Z.
Rețineți că atunci când accesați funcția plot3d ca parametri X și Y. specificând o rețea dreptunghiulară, parametrul t este specificat de două ori, deoarece ambele funcții sin și cos depind de o variabilă t (a se vedea lisțiunea 5.1, figura 5.1).
Listing 5.1. Schema funcției Z = sin (t) cos (t) cu ajutorul plot3d
Acum hai să complicăm puțin sarcina. Construim o suprafață a cărei ecuație este dată de două variabile independente.
Construiește un grafic al funcției Z = 5y 2 x 2.
5.1. Funcțiile plot3d și plot3d1
Fig. 5.1. Graficul grafic al funcției Z = sin (t) cos (t)
Mai întâi, să specificăm matricele X și Y.
Apoi se formează matricea valorilor funcției Z (x i; y j), utilizând instrucțiunea for pentru buclă. Aici i este parametrul buclă care va trece prin toate valorile arrayului X și j este parametrul buclă care va cartografia fiecare valoare a matricei X în schimb la toate valorile matricei Y.
Astfel, vor fi calculate mai întâi toate valorile funcției Z cu Y variabilă (de la prima la ultima valoare a matricei) și prima valoare a matricei X. Apoi, cu a doua valoare a matricei X, etc.,
Recall, lungimea specifică numărul de elemente ale matricei X (Y) (vezi capitolul 2).
În cele din urmă, pentru a construi suprafața, ne întoarcem la funcția plot3d1 (a se vedea
5.2, figura 5.12).
După cum puteți vedea din exemplu, folosirea doar a funcției plot3d pentru afișarea grafică a indicatorilor care depind de două variabile independente este destul de dificilă. În Scilab, există mai multe comenzi proiectate pentru a facilita crearea unei rețele rectangulare: genfac3d și eval3dp.
Cea mai simplă dintre ele prin sintaxă este funcția genfac3d:
Aici, xx, yy, zz mărimea rezultată a matricei (4; n 1, m 1), unde xx (:, i), yy (:, i) și zz (:, i) coordonatele fiecărei celule dintr-o grilă dreptunghiulară;
x vector al coordonatelor x de mărimea m;
y vector al coordonatelor y de mărimea n;
z este o matrice cu mărimea (m; n) a valorilor funcției Z (x i; y j).
Construiți un grafic al funcției Z = sin (t) cos (t).
Definiți o matrice a parametrului t și calculați valorile funcției Z = sin (t) cos (t). Creăm o rețea dreptunghiulară folosind comanda genfac3d (vezi Listing 5.3).
Listing 5.3. Creați o rețea dreptunghiulară folosind comanda genfac3d și plotați graficul utilizând funcția plot3d
Pentru a forma graficul, ne întoarcem la funcția plot3d (vezi Figura 5.1). Dezavantajul comenzii genfac3d este că încă nu simplifică
lucrați cu plotul funcției3d, dacă suprafața este dată de o funcție a două variabile. În acest caz, trebuie să utilizați comanda eval3dp:
Xf, Yf, Zf - mărimea rezultată a matricei (4; n 1, m 1), unde xx (:, i), yy (:, i) și zz (:, i) coordonatele fiecărei celule dintr-o grilă dreptunghiulară;
Distribuie o funcție definită de utilizator care specifică un grafic tridimensional;
5.1. Funcțiile plot3d și plot3d1
vectorul p1 de mărimea m;
p2 este un vector cu dimensiunea n.
Să ilustrăm acțiunea comenzii eval3dp cu exemplul următor.
Construiți un grafic dat de următoarele ecuații: x = p 1 sin (p 1) cos (p 2), y = p 1 cos (p 1) cos (p 2), z = p 1 sin (p 2).
În primul rând, definim matricea valorilor parametrilor p 1 și p 2. Apoi, creăm funcția scp, care stabilește graficul.
Amintiți-vă că funcțiile din Scilab sunt create folosind comanda deff:
unde s1, s2. lista parametrilor de ieșire, adică variabile la care va fi atribuit rezultatul final al calculelor;
funcția newfun numele funcției care va fi creată, va fi utilizată pentru apelarea acesteia;
e1, e2. parametrii de intrare.
Rețineți că comanda deff este scrisă numai în trei rânduri pentru a facilita citirea înregistrării (a se vedea Listing 5.4).
Listing 5.4. Creați o rețea dreptunghiulară utilizând eval3dp și plotați graficul folosind plot3d
p2 = linspace (0,2 *% pi, 10); (p1) * cos (p2) ";" y = p1. * cos (p1) cos (p2) ";
"z = p1. * sin (p2)"]); [Xf, Yf, Zf] = eval3dp (scp, p1, p2); plot3d (Xf, Yf, Zf);
Acum creați o rețea dreptunghiulară utilizând comanda eval3dp și plotați graficul referindu-vă la funcția plot3d (a se vedea Figura 5.13).