Titlul lucrării: Graficarea în Mathcad
Domeniu: Informatică, Cibernetică și Programare
Descriere: Pentru aceasta trebuie să cunoaștem ecuațiile graficelor tangente și normale. Nu i-am cunoscut, așa că a trebuit să mă întorc la internetul atotputernic. În el am găsit site-ul, da, stochează browserul Mozilla Firefox puternic, care mi-a arătat servitorul stupid, ecuațiile funcțiilor de care aveam nevoie.
Mărime fișier: 181,5 KB
Lucrarea a fost descărcată: 38 de persoane.
Ministerul Educației și Științei al Federației Ruse
UNIVERSITATEA TEHNICĂ DE STUDIU RYBINSKY STATUS numită. P. A. Solovyev
Facultatea de Inginerie Radio, Electronică și Informatică
informatică
Student al grupului SPD-13 Pestov VV
Semnatura codului, data
Profesor Pinaev V.N.
Pentru o funcție dată.
1. Construiește un grafic al funcției și al graficelor primului și celui de-al doilea derivat în coordonate comune.
2. Construiați curbele tangente și normale la funcția în punctul (x 0 = 3) 0.
3. Găsiți punctele extreme extreme locale ale funcției f (x) și punctele de inflexiune (puncte staționare).
4. Determinați valoarea funcției la punctele staționare.
5. Definiți primitivul + c și construiți graficele familiei primitive.
1. Construiește un grafic al funcției și al graficelor primului și celui de-al doilea derivat în coordonate comune.
Pentru a construi un grafic al unei funcții și al celor două derivați ai acesteia în Mathcad, trebuie să obținem primul și al doilea derivat al derivatelor. Puteți să o faceți singur, fără a utiliza programe:
(x-x) = e (x) = x * (e)
Acum că am calculat atât derivate, este timpul să construim grafica în Mathcad. Asta sa dovedit la mine, este posibil să vedem în figura 1:
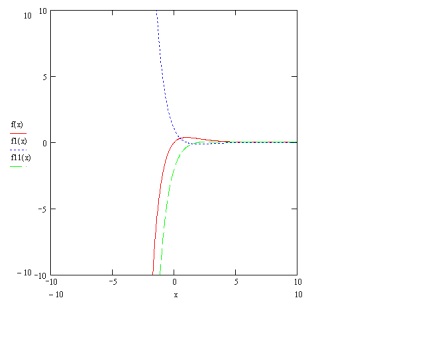
Linia roșie arată graficul funcției în sine, verde și albastru - graficele primului și al doilea derivat, respectiv.
Deci, primul lucru este făcut.
2. Este necesar să se construiască graficele tangente și normale în graficul de funcții.
Ecuația tangentei este după cum urmează:
y = f '(x 0) * x + f (x 0) -f' (x 0) * x 0
Ecuația normală are forma:
y = f (x 0) - (x-x 0) / f '(x 0)
Unde x 0 = 3 (punctul dat de condiție).
Acum că am ecuații, rămâne să le scriu în programul Mathcad. Iată graficele pe care le am (Fig.2):
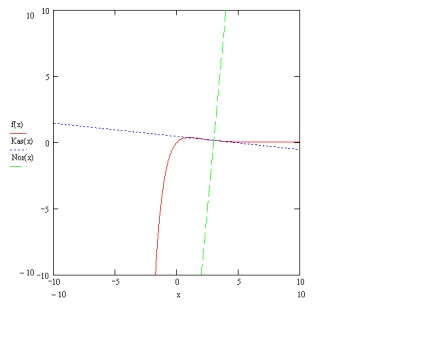
Linia roșie este graficul funcției, albastrul este tangent la graficul de la punctul x 0. verde este normal față de grafic la punctul x 0.
Sarcina 2 poate fi considerată îndeplinită.
3. Găsiți punctele extreme extreme locale ale funcției f (x) și punctele de inflexiune (puncte staționare).
Pentru a găsi punctele de extremă locală, este necesar să echivalăm primul derivat al funcției la zero.
f '(x) = 0; e - x * (1 - x) = 0; 1- x = 0;
x = 1 este un punct critic, este și staționar (punctul critic este punctul în care funcția își schimbă direcția: dacă crește, începe să scadă (în cazul meu) și invers). Un punct staționar este un punct la care derivatul este zero.
Cu această sarcină, m-am descurcat și eu.
4. Determinați valoarea funcției la punctele staționare.
Ei bine, e destul de simplu. Este suficient să înlocuiți punctul x = 1 în ecuația funcției:
Am decis să prezint valoarea în formă numerică, va fi egală cu:
Deci, această slujbă este terminată, ultima este lăsată.
5. Definiți primitivul + c și construiți graficele familiei primitive.
Mi-am permis să nu schimb limba, pentru că nu am vrut să încalc întreaga formă fermecătoare a acestui site. Acum am acum ecuația antiderivativă. Dar trebuie să construiesc o familie de primitivi. Am început deja să-mi fac griji, pentru că am o singură formulă și trebuie să construiesc câteva diagrame, până când am fost invitat să-l schimb pe Constant. Și acum scriu formule în Mathcad și, pentru un miracol, graficele familiei primitive sunt gata pentru mine (Figura 3):
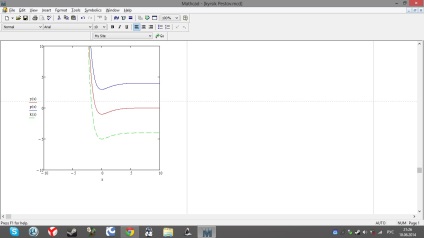
Linia roșie indică prototipul, unde const = 0, iar pentru celălalt const = 4; -4, respectiv.
Așa că treaba mea se termină. E timpul să rezumăm.
În cursul acestei lucrări, am învățat un program minunat ca Mathcad. a dobândit puțină abilitate în manipularea lui și, din nou, și-a convins o asemenea creație grandioasă a omului ca pe Internet, căci înaintea lui trebuie să ne cădem în genunchi, pentru că acesta este urmașul nostru, care aproape ne înrobește. Și eu, un servitor despicabil, mă plec înaintea lui. Și, de asemenea, îi mulțumesc mentorilor mei, Vladimir Nicolaevici Pinaev și Dmitriy Sergheiev Shalaev, datorită cărora, un astfel de servitor pe care l-am învățat și am reușit să-l stăpânesc pe programul Mathcad.