Desenați o diagramă pentru calcul în funcție de sarcină.
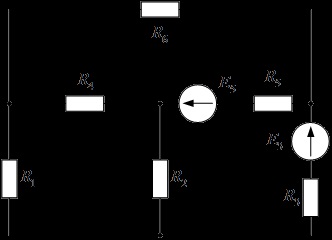
1. Ecuații conform legilor din Kirchhoff.
Alegem și indicăm direcțiile pozitive ale curenților de ramificație pe circuit.
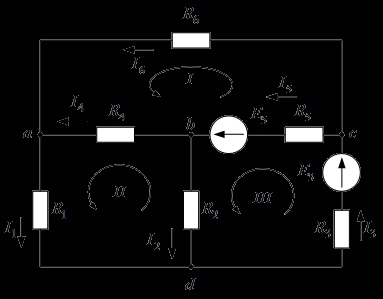
Lanțul conține un nod și ramuri. Este necesar să se determine 6 curenți. Circuitul conține surse curente. Numărul de ecuații conform legii 1 Kirchhoff este egal cu numărul de noduri minus unul, adică . Celelalte trei ecuații sunt conform celei de-a doua lege a lui Kirchhoff :.
Ecuații conform legii 1 Kirchhoff
Ecuațiile conform legii a doua a lui Kirchhoff:
Substituim valorile numerice ale cantităților pe care le obținem
2. Calculați curenții în ramuri prin metoda curenților de contur.
Alegem și arătăm curenți de contur pe circuit.
Să formuleze un sistem de ecuații cu privire la curenții de contur
Înlocuim valorile numerice
Rezolvăm sistemul de ecuații rezultat cu ajutorul determinanților:
,
determinarea curenților de contur
Acum, în conformitate cu direcțiile selectate ale curenților de ramură, le găsim valorile folosind valorile curenților de buclă:
3. Metoda de potențial nodal.
Presupunem că potențialul nodului este zero. Vom compune sistemul de ecuații prin metoda potențialului nodal cu privire la:
Să calculăm coeficienții sistemului:
- conductivitatea intrinsecă a nodurilor:
Conductibilitatea totală a nodurilor:
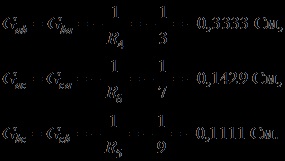
Rezolvăm sistemul de ecuații:
Calculăm curenții de ramură conform legii generalizate a lui Ohm
4. Definirea rezistenței de intrare a ramificației față de ramura 2.
Înlocuim "triunghiul" rezistențelor cu o stea "echivalentă".
4. Să verificăm balanța energetică a circuitului.
Să facem un echilibru de putere. Ecuația echilibrului energetic reflectă egalitatea de putere dată de surse și consumată de consumatori.
. balanța puterii converge. Inexactitatea se datorează erorii în calcule.
6. Diagrama potențială.
Construim o diagramă potențială pentru următorul contur:
Luăm potențialul punctului de a fi zero ,,,