O curbă a avionului este o linie, fiecare punct din care aparține aceluiași avion. În caz contrar, linia curbă se numește linia spațială (linia de helix, liniile de intersecție a două suprafețe, dintre care cel puțin una este o suprafață curbată).
Liniile regulate sunt descrise prin ecuații și sunt împărțite în algebre algebrale al doilea și superioare și cele transcendente, descrise prin funcții trigonometrice. Ordinea curbei liniei este gradul ecuației sale sau numărul punctelor de intersecție a curbei liniei cu linia dreaptă (pentru curbe plane) sau numărul punctelor de intersecție cu planul (pentru liniile spațiale). Curbe de ordinul doi sunt uneori numite conuri.
Liniile cu linie (sau contururile) se numesc linii curbe compuse, ale căror arce sunt definite secvențial prin perechi de puncte ale bypass-ului. Dacă se poate construi o comună tangentă la articulații, atunci conturul este numit neted. Liniile circulare sunt linii, a căror construcție se poate realiza cu o busolă (ovală, ovoidă, curl etc.).
Curbele locale se numesc linii regulate, atunci când se desenează, ele folosesc modele (elipsă, parabola, hiperbola, etc.).
Curbele ciclice ale liniei sunt liniile care se repetă în procesul de formare (cicloid, epicicloid, hipocicloid, etc.).
Liniile curbe netede constau din puncte obișnuite.
Punctele obișnuite ale unei curbe a unei linii sunt puncte în care este posibilă construirea unei singure tangente la o curbă a unei linii. Dacă curba conține puncte singulare, linia se numește nonsmooth.
Liniile echidistant și echantangent sunt liniile echidistant de la o anumită curbă a liniei și repetând forma acesteia.
Liniile aproximative sunt linii care sunt aproximativ înlocuite
alte linii mai convenabile pentru plotare (de exemplu, o elipsă este înlocuită uneori de o ovală).
Curbele de linie și spațiu
Cel mai adesea, tehnica folosește linii curbe curbe, care pot fi plane și spațioase. Acestea includ o elipsă, parabolică, hiperbolă, evolventă, cicloida, o linie în spirală, și altele, care sunt exemplificate în Figura 1. Metode pentru construirea liniare curbe sunt considerate, de obicei, în cursul tehnic
Evolventa - traiectoria punctului tangent, rulând fără alunecare de-a lungul circumferinței. Uneori se numește greșit numirea unui cerc.
Un sinusoid este o curbă care este descrisă de ecuația y = sin x.
Hyperbola este locul geometric al punctelor a căror diferență de distanțe față de două puncte, numite foci, este o valoare constantă.
O linie elicoidală este o traiectorie a unui punct care se deplasează de-a lungul unei generatoare a unui cilindru, a unui con sau a unui torus, în timp ce generatorul se rotește uniform în jurul axei acestor suprafețe.
Elipsa este locusul punctelor a căror sumă de distanțe la două puncte, numite foci, este o constantă.
O parabolă este locusul de puncte echidistant de la un punct numit focalizare, și o linie dreaptă numită directrix.
Cycloidul este traiectoria unui punct dintr-un cerc care este rulat fără alunecare de-a lungul unei linii drepte. În construcția epi- și hipocicloidelor, circumferința este rulată în jurul circumferinței.
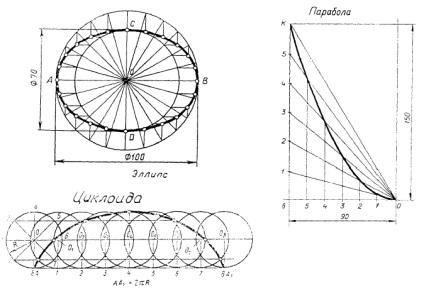
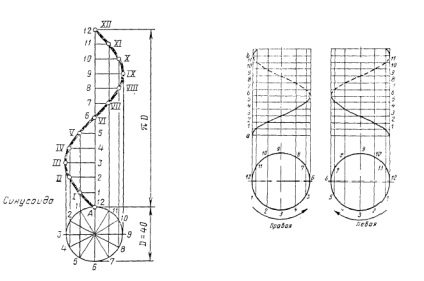
Figura 1 - Exemple de curbe locale
Construirea de proiecții ale curbei unei linii
Proiecțiile curbei liniei au următoarele proprietăți:
În cazul general, proiecția curbei liniei este o curbă;
Dacă punctul aparține curbei liniei, atunci proiecția acesteia
aparțin acelorași proiecții ale curbei;
Tangenta liniei curbe este proiectata in linia tangenta
proiecții ale curbei liniei.
EXEMPLUL 1 Construiți proiecțiile liniei elicoidale cilindrice drepte care trece prin punctul suprafeței cilindrului.
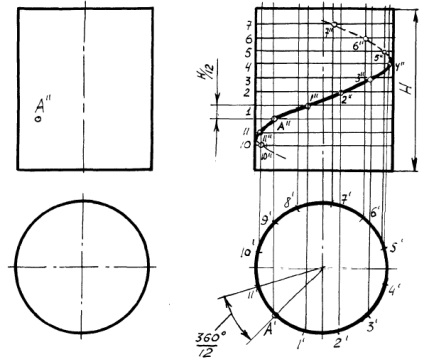
Figura 2 - Exemplul 1.
SOLUȚIE. Gasim punctul A /. Pornind de la punctul A /. împărțiți circumferința bazei cilindrului în 12 părți. Înălțimea cilindrului H este împărțită în 12 părți, pornind de la punctul A //. La intersecția liniilor verticale și orizontale cu același nume găsim punctele liniei șuruburilor, care sunt bine conectate (figura 2).
Informații generale despre suprafețe
Suprafața este locul geometric al unei linii care se deplasează în spațiu conform unei anumite legi. Această linie este numită generatrix. Poate fi dreaptă, atunci suprafața formată la ea se referă la clasa celor condamnați. Dacă generatorul este o linie curbă, suprafața este considerată neliniară. Linia de-a lungul căreia se deplasează generatorul se numește ghidaj. Ca și cea din urmă, uneori se utilizează o urmă a suprafeței.
Determinantul unei suprafețe este setul de condiții care definesc o suprafață în spațiu.
Suprafața este considerată dată dacă este posibilă construirea proiecțiilor oricărui generator. Una și aceeași suprafață poate fi formată prin mișcarea diferitelor linii. De exemplu, sfera este formată prin rotirea unui cerc în jurul diametrului său.
Suprafețele considerate mai jos sunt clasificate după cum urmează.
I. Sunt influențate suprafețele de rotație.
II. Suprafețele de rotație sunt neliniar.
Tor (circular, parabolic, eliptic).
Ellipsoid (alungit și comprimat).
Suprafața revoluției este de formă generală.
III. Suprafețe cu un plan de paralelism.
IV. Suprafețele date de schelet.
Suprafața rotativă de rotație
Toate suprafețele din această clasă sunt formate prin rotirea unei linii drepte în jurul unei alte linii drepte. Două linii drepte pot ocupa trei poziții diferite unul față de celălalt. Fiecare dintre ele are propria suprafață de revoluție.
1
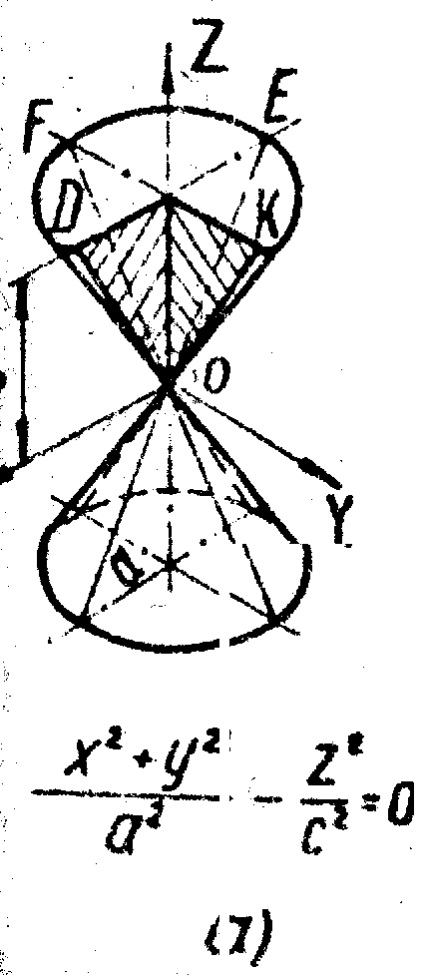
.Conul se formează prin rotirea liniei drepte OD în jurul axei Z care se intersectează cu ea (figura 3, a). Planurile de coordonate XOZ și YOZ disecă conul de-a lungul liniilor drepte intersectate OD, OE, OK și OF; planul XOZ dă punctul O în secțiune; avionul. paralel cu XOY, intersectează circumferința (DFEK).
Pentru a construi un punct aparținând curbei suprafeței, suprafața sa este situată pe proeminențele liniei situate pe această suprafață.
Cone participă la formarea formei antenei de model radiație, poziția suprafeței obiectului în spațiu, antena și hrana acestuia, conul difuzorului, reflectorul cavitate undelor radio, tuburi electronice și tuburi cu vid, fibre, piese de echipamente de vacuum și așa mai departe.
2
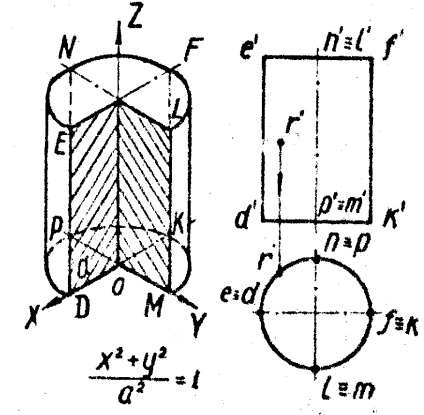
.Cilindrul este format prin rotirea liniei drepte ED în jurul axei Z paralele cu ea (Figura 3, b, c)
XOz și YoZ planuri paralele se intersectează de-a lungul drepte ED lui, FK, NP, LM, și planul XOY și paralelă cu ea - de-a lungul cercuri DPKM si (ENFL).
Cilindrul este utilizat pentru a forma ghiduri de undă, antene, amortizoare de amortizare pentru instrumente, oglinzi laser, carcase de senzori și așa mai departe.
3. Se formează un hiperboloid cu o singură pătură prin rotirea unui ED drept în jurul axei Z care se intersectează cu el (Figura 4).
Avionul xOz și YOZ cruce hiperbola lui FK, LM, PQ și RS, și planul XOY și paralel cu acesta - în cercuri (GU, FPLR și KQMS). La punctele de rotație D și E ale proiecțiilor d și e sunt deplasate de-a lungul circumferinței, iar proeminențele d și e - de-a lungul liniilor drepte paralele cu axa X. Punctul unei drepte U DE, situată cel mai apropiat de axa de rotație, descrie un cerc UU1 cel mai mic diametru. Acest cerc se numește gâtul suprafeței. Razele care proiectează o suprafață o ating în punctele care formează linia de contur. Proiecția corespunzătoare a acestei linii se numește conturul suprafeței.
Un hiperboloid cu un singur strat are câteva stâlpi radio. Formează, de asemenea, forma alimentatoarelor vibratoare utilizate în automatizarea industrială, camă, conectori de contact și așa mai departe.
La această clasă se află în principal suprafețele formate prin rotirea curbelor de ordinul doi.
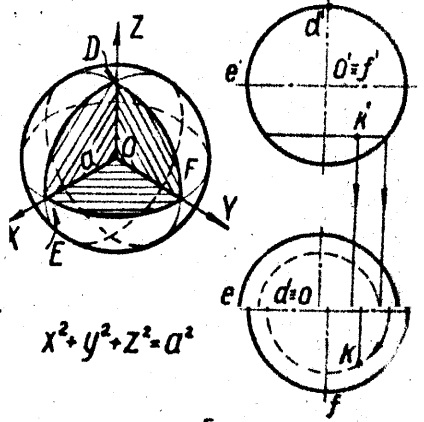
1. Sfera este formată prin rotirea cercului în jurul diametrului său (Figura 5)
Orice avion intersectează sfera într-un cerc. O schiță a proieciei frontale a sferei este numită meridianul principal. un contur al proiecției orizontale de către ecuator. Proeminențele punctului K care se află pe suprafața sferei aparțin proiecțiilor cercului orizontal desfășurate pe sferă.
Sfera formează forma antenei, radiomodul și radiatorul antenei, capul microfonului, contactele releului și așa mai departe. Sfera este suprafața poziției obiectului în spațiu.
2. Un torus circular este format prin rotirea unui cerc în jurul unei axe situate în planul acestui cerc și care nu este diametrul său. Astfel, sfera poate fi privită ca un caz special al torusului. Distingeți tor-ring-ul. Când axa de rotație nu se intersectează cu cercul de generare și cu butucul torus.
În domeniul radiotehnicii, se utilizează și un torus parabolic și eliptic.
Un torus parabolic se formează prin rotirea unei parabole în jurul unei linii situată în planul acestei parabole și nefiind axa sa focală.
Un torus eliptic este format prin rotirea elipsei pe o linie dreaptă situată în planul acestei elipse și nefiind axa sa.
Suprafețele torsionale au modele de directivitate a antenei, suprafețe de poziționare a obiectelor în spațiu, antene și jgheaburi, ghiduri de undă, rezonatoare, difuzoare și așa mai departe.
Un elipsoid este format prin rotirea unei elipse in jurul axei sale mici sau mari. În primul caz, se obține un comprimat (Figura 6, a), iar în al doilea caz se obțin elipsoidele alungite de rotație (fig.6, b).
Avioanele XOZ și YOZ le traversează de-a lungul elipsei DE și EF, iar planul XOY de-a lungul circumferinței DF.
Forma elipsoidului are oglinzi de antene și lasere, emițătoare de antenă, suprafețe de poziționare și așa mai departe.
Un hiperboloid cu două colțuri se formează prin rotirea hiperbola DE în jurul axei sale reale FF1 (Figura 7).
Planul XOZ și YOZ îl traversează peste hyperbola DE și KE; planul XOY dă un punct imaginar O în secțiune.
Forma sa are oglinzi ale antenei, suprafața poziției obiectului în spațiu și așa mai departe.
5. Paraboloidul se formează prin rotirea OD a parabolei în jurul axei sale focale (Figura 8).
Oglinzile antenei și laserelor sunt cele mai multe ori parabolice.
6. Suprafața de rotație a formei generale este formată prin rotația unei curbe arbitrare.
Suprafețe cu un plan de paralelism.
Toate suprafețele din această clasă sunt conduse.
1. Cilindroidul se formează prin deplasarea unei linii drepte de-a lungul a două ghidaje curbate, când generatorul rămâne paralel cu planul dat. Forma cilindrului are câteva grafice volumetrice utilizate în teoria controlului optim, precum și ghidurile de undă.
2. Conoidul formează o linie dreaptă de-a lungul liniei curbe și liniei drepte, când generatorul rămâne paralel cu planul dat. Un caz particular al conoidului este o spirală dreaptă formată prin deplasarea unei linii drepte de-a lungul helixului și a axei acestuia, atunci când generatorul rămâne paralel cu planul dat.
3. Se formează un paraboloid hiperbolic sau un plan de înclinare prin deplasarea unei linii drepte de-a lungul a două linii drepte intersectate, atunci când generatorul rămâne paralel cu un anumit plan. Suprafața rezultată are o formă de șa (figura 9).
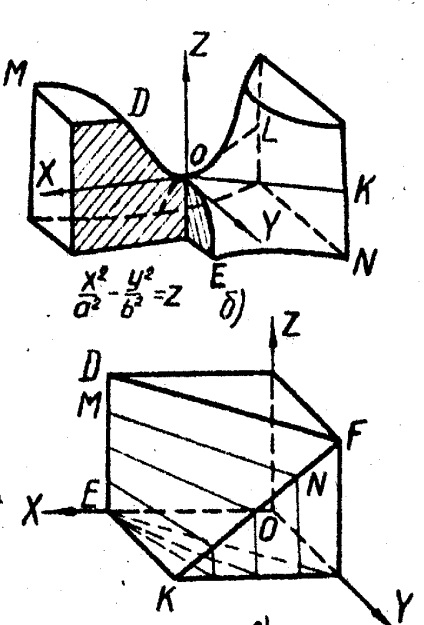
Avioanele XOZ și YOZ traversează această suprafață de-a lungul parabolelor OD și OE; planuri paralele cu XOZ și YOZ, dau și parabole în secțiune; planul XOZ intersectează suprafața de-a lungul a două linii drepte intersectate OL și OK, iar planurile paralele cu XOZ sunt traversate de hiperbola (EN și DM).
Suprafețele date de schelet.
Acestea includ suprafețele a căror formare nu este supusă unei anumite legi geometrice. Aceste suprafețe sunt definite de un cadru - o familie de linii aparținând acestora și paralele cu planurile de coordonate (figura 10).
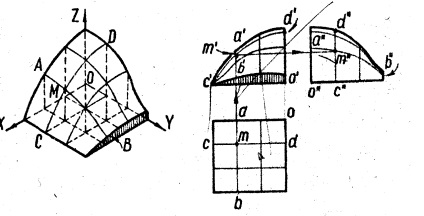
În Fig. 10 prezintă graficul volumetric utilizat în radiotehnică. Suprafața este definită de linii curbe, o familie din care (CD) este paralelă cu planul XOZ, iar cealaltă (AB) este planul YOZ. Punctul M al suprafeței este definit ca punctul de intersecție al curbelor AB și CD.
În electronica și automatizarea radioului există suprafețe de ordinul doi de formă generală: conul și cilindrul eliptic, cilindrii parabolici și hiperbolici și așa mai departe.
Lista literaturii utilizate.
Anisimov IK Rezumate ale prelegerilor privind geometria descriptivă. - R. 1970.
Frolov SA Geometria descriptivă: un manual pentru licee. - M. Machine Building, 1983.