Graficul grafic al funcției y = tgx
Dacă știți cum să lucrați cu cercul trigonometric. atunci puteți construi cu ușurință o funcție grafică.
Sper că îți amintești unde se află axa tangentă ...
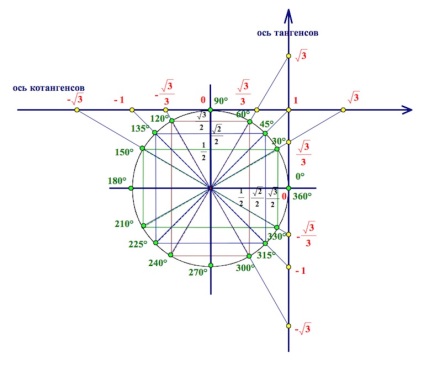
Privind la imaginea se poate vedea în mod clar că valoarea tangentă în cadranele I și III coincid cu valorile corespunzătoare ale sferturi de culoare cafenie II și IV. (De exemplu, etc.)
Transferăm valorile de bază ale unghiurilor reprezentate pe cerc, de exemplu, din sferturile I și IV și valorile tangente corespunzătoare la planul de coordonate.
Pe axa absciselor, complotăm unghiul în radiani, de-a lungul ordinii - valorile tangentei unghiului.
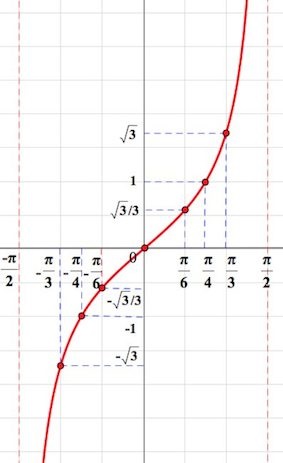
Punctele de pe planul de coordonate ne determină o curbă lină. Acesta este graficul funcției pe.
Fiți atenți! Tangenta nu exista in puncte. Putem doar "să ajungem" în mod arbitrar la aceste valori.
Fragmentul de mai sus al graficului tangent va fi o ștampilă pentru noi. Replicând acest fragment, obținem următorul grafic al funcției:
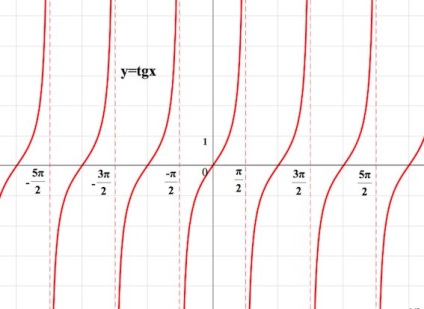
Graficul grafic al funcției este simetric în raport cu originea.
Graficul grafic al funcției y = ctgx
Așa cum am construit graficul folosind cercul trigonometric, am putea construi și.
Procedăm oarecum diferit.
În funcție de formulele de reducere sau, care este același lucru, ce.
Din care concluzionăm că graficul graficului este primit compensat la unitățile din stânga, și în care graficul „înclinat“ în raport cu axa (bou) cu un factor de -1.
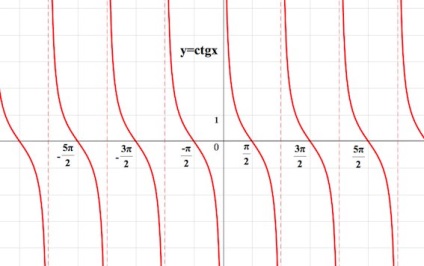
Graficul grafic al funcției este simetric în raport cu originea.
Site-ul lui A. Larin EgeTrener - O. Sebedash Matematica? Este ușor! CSE? Ok! - I. Feldman
