Să fie diferențiată la punctul x. Prin definiția derivatului. Prin teorema privind conectarea limitei cu infinitezimale. unde la. Noi multiplicăm ambele părți prin # 8710; x:
(1), unde # 8710; x → 0 ,. .
Comparați aceste infinite:
În cazul în care. atunci # 8710; x - l.m. de aceeași ordine
2) - l.m. ordinea superioară a micșorării # 8710; x.
Astfel, creșterea funcției # 8710; y constă din 2 x termeni: prima este partea principală a creșterii funcției. liniar cu privire la # 8710; x; iar cel de-al doilea termen este infinitezimale de ordin mai mic decât # 8710; x.
Definiția. Diferența unei funcții la un punct x este produsul derivatului în acest punct prin incrementarea argumentului # 8710; x.
Să găsim diferența funcției. pentru că . atunci. care este. (3)
Diferența dx a variabilei independente x coincide cu incrementul # 8710; x.
Formula (2), având în vedere (3), ia forma: (4) este diferența funcției.
Prin urmare - (desemnarea lui Leibniz).
Derivatul unei funcții poate fi considerat ca fiind raportul dintre diferențialul funcției și diferențialul variabilei independente.
§13. Semnificația geometrică a diferențialului.
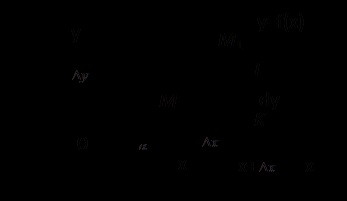
Desenăm o tangență la graficul funcției în punctul M (x, y).
# 945; Este unghiul de înclinare a tangentei față de axa Ox.
Da x incrementul # 8710; x. atunci funcția va crește # 8710; y. Pe curbă obținem punctul M1 (x + # 8710; x, y + # 8710; y), KT este creșterea ordinii tangentei.
| |
Diferența funcției în x este egală cu creșterea ordinii tangentei la tranziția de la punctul cu abscisa x până la punctul cu abscisa x + # 8710; x.
Invarianța formei diferențialului (independența formei înregistrării diferențiale).
1) Să presupunem că. x este o variabilă independentă
2) Să presupunem că. x = x (t) este o funcție a lui t.
Este o funcție complexă, x este un argument intermediar.
(prin regula pentru diferențierea unei funcții compuse)
În formulele (1) și (2), forma înregistrării diferenței este aceeași. Proprietatea diferențialului are aceeași formă de înregistrare, indiferent dacă x este o variabilă independentă sau o funcție a altei variabile se numește invarianța formei diferențialului.