2. Imaginea operațională a unei tensiuni constante.
3. Diagrama operatorului de substituție este prezentată în Fig. 9.9. Calculul circuitului operatorului se efectuează prin metoda curenților de buclă:
Capacitorul pe diagrama operatorului este reprezentat de două elemente. Pentru calcul, este mai bine să se ia în considerare un contur în care imaginea intră în ecuație (a se vedea Figura 9.9). Apoi, obținem
.
Calculați metoda curentă în ramurile circuitului prezentat în Fig. 9.9. Circuitul are o sursă constantă de curent constant A. Parametrii elementelor: Φ; dl; Ohmi.
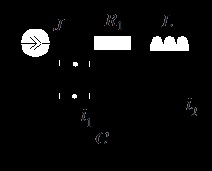
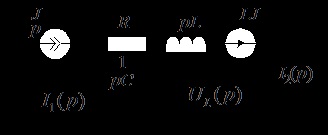
1. Condiții inițiale independente:
2. Imaginea operatorului curentului de referință.
3. Diagrama operatorului este prezentată în Fig. 9.11. Calcularea sa se efectuează în conformitate cu ecuațiile lui Kirchhoff:
;
;
Inductorul este reprezentat de rezistența operatorului și de emf din condițiile inițiale. Pentru a determina, să scriem ecuația conform celei de-a doua lege a lui Kirchhoff pentru circuitul indicat pe diagrama:
,
Calculul suplimentar este posibil în cifre:
;
.
4. Putem efectua tranziția către originale prin teorema descompunerii. Pentru a alege o modificare a teoremei de expansiune, definim rădăcinile polinomului numitor, adică rezolva ecuația. Rădăcini Toate rădăcinile sunt simple, deci putem folosi formula (9.17). Numitorul expresiei pentru cele două rădăcini, prin urmare
,
;
; .
Numitorul funcției are o a treia rădăcină zero, atunci
,
; ;
; .
Ca rezultat, obținem
Tensiune la bobină și sursă
,
; .
Graficele dependențelor actuale din ramuri sunt prezentate în Fig. 9.12, a, iar tensiunile pe bobină și condensator sunt prezentate în Fig. 9.12, b.

1. Imaginea tensiunii de intrare (vezi tabelul 9.1). Condițiile inițiale sunt zero.
2. Diagrama operatorului este prezentată în Fig. 9.14. Imaginea operațională a curentului
3. Trecerea la original se face prin teorema descompunerii. Rădăcinile numitorului.
Dacă numitorul are rădăcini simple și o rădăcină de multiplicitate (cu aceleași rădăcini), atunci teorema de descompunere poate fi scrisă în formularul (9.19). În special, pentru două rădăcini identice, expresia (9.19) are forma
Pentru o rădăcină simplă, prin teorema descompunerii
.
Combinând componentele, obținem curentul dorit
Tranziția se poate face conform tabelului 9.1.
Este necesar să se determine legea variației tensiunii pe condensator pentru circuitul prezentat în Fig. 9.15. La circuit se aplică tensiunea sinusoidală la parametrii elementelor de circuit: uF; Ohmi. În calcul, utilizați o imagine complexă a tensiunii sinusoidale.
1. Calculul stării staționare înainte de comutare se realizează printr-o metodă simbolică:
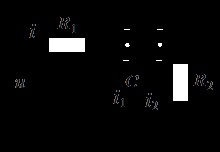
Imaginea operațională a componentei libere a curentului
.
Rădăcinile polinomului numitor:
Trecerea de la imagini la originale este realizată de teorema descompunerii. Componenta curentă liberă:
Expresia curentului în circuit este scrisă ca sumă a componentelor de curent liber și forțat:
1. Scrieți formulele pentru transformarea directă și inversă Laplace.
2. Formulează proprietățile transformării Laplace.
3. Cum să identificăm originalul din imaginea sa?
4. Cum să identificați o imagine dintr-un original cunoscut?
5. Formulați teorema descompunerii și descrieți procedura de aplicare a acesteia.
6. Scrieți ecuațiile lui Kirchhoff și ecuațiile elementelor ideale în forma operatorului.
7. Cum se creează o schemă a operatorului pentru calcularea procesului tranzitoriu?
8. Cum se creează o schemă a operatorului pentru calculul componentei libere a procesului tranzitoriu?
9. Care este procedura de calcul al schemei de substituție a operatorului?
9. Care sunt metodele de calculare a metodei tranzitorii de către operator?
11. Să formuleze avantajele și dezavantajele metodei operator și fiecare tehnică separată.