1. Cu mișcarea de translație a legăturii, rezultatul forțelor de inerție ale tuturor maselor elementare
Se aplică în centrul S al masei de legătură și este direcționat în direcția opusă accelerației centrului S al masei de legătură (Figura 12).
2. Dacă legătura efectuează o mișcare de rotație în jurul axei, coincide cu centrul de masă, atunci forțele inerțiale ale tuturor maselor elementare pot fi reduse la o pereche de forțe cu un moment (Figura 13):
unde este momentul static al inerției legăturii față de axa care trece prin centrul de masă perpendicular pe planul de mișcare.
Semnul "-" din formula pentru Min indică faptul că momentul este direcționat în direcția opusă accelerației unghiulare.
Momentul de inerție al corpului Js în raport cu o axă este o cantitate egală cu suma produselor din masele elementare ale acestui corp pe pătrat de distanța lor față de această axă:
3. Legătura efectuează o mișcare complexă (Figura 14). În acest caz, mișcarea legăturii este descompusă într-o translatare portabilă cu viteză și accelerare a centrului de masă și a mișcării relative de rotație în jurul centrului de masă.
Forțele de inerție ale tuturor maselor elementare sunt reduse la forța de inerție rezultantă și la perechea de forțe cu momentul. .
Forța de inerție este aplicată la centrul S al masei de legătură și este direcționată în direcția opusă accelerației centrului de masă; Momentul inerției este îndreptat în direcția opusă # 949; .
4. Legătura se rotește în jurul unei axe care nu trece prin centrul masei de legătură (Figura 15).
Considerăm acest caz drept un caz general al unei mișcări complexe a legăturii: forțele inerțiale ale tuturor maselor elementare se reduc, de asemenea, la forța inerțială rezultantă și la forțele pereche cu momentul.
1.5.2 Determinarea finelor și minelor pentru mecanismul de ghidare-manivelă (Figura 16)
Fie ca centrul de masă 1 al legăturii S1 să fie la punctul A (în centrul de rotație al legăturii 1), S3 coincide cu punctul C; S2 - în mijlocul legăturii 2.
Pentru a determina Fini și Mini; este necesar să se cunoască accelerația liniară a centrelor de masă și accelerația unghiulară a legăturilor, pentru care (în soluția grafică a problemei) este necesar să se construiască planuri de viteză și accelerare (fig.17, a, b).
Legătura 1 efectuează o mișcare uniformă de rotație (din moment ce # 969; 1 = const. atunci). Centrul de masă este fix și ca = 0, prin urmare, Fin1 = 0.
Linkul 2 efectuează o mișcare paralelă plană:
. .
Pentru a găsi accelerația punctului S2, folosim teorema similarității:
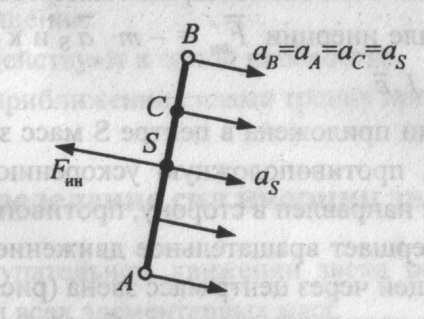
Fig. 12. Forța de inerție a legăturii cu mișcarea sa de translație (momentul forțelor de inerție este zero)
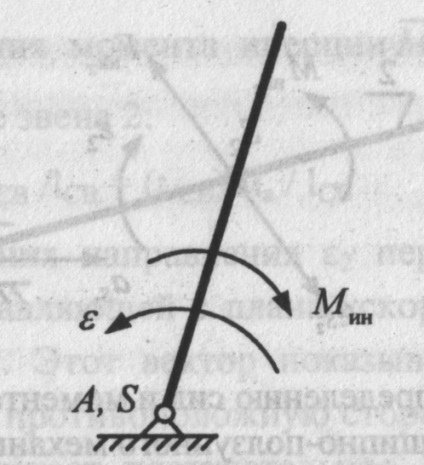
Fig. 13. Momentul inerției unei legături atunci când aceasta se rotește în jurul unei axe care trece prin centrul masei de legătură (forța de inerție este zero)
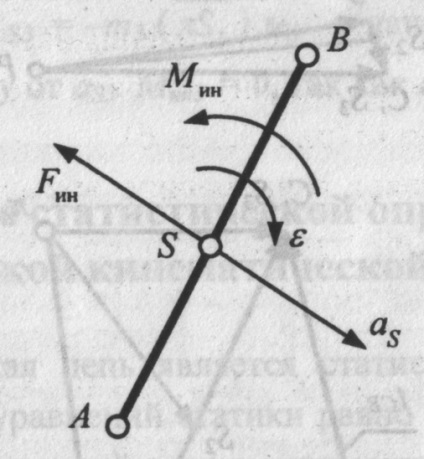
Fig. 14. Forța și momentul forțelor de inerție ale unei legături care efectuează o mișcare complexă
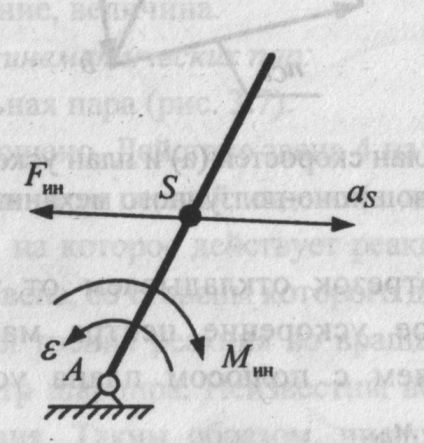
Fig. 15. Forța de inerție și momentul inerției unei legături care se rotește în jurul unei axe care nu trece prin centrul de masă al legăturii
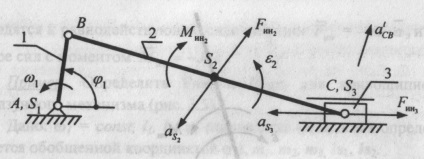
Ris16. Pentru a determina forțele și momentele forțelor de inerție ale mecanismului de glisoare
Fig. 17. Planul de viteză (a) și planul de accelerație (b) al mecanismului glisorului
Am amânat segmentul găsit din punctul c. Pentru a găsi accelerația absolută a centrului de masă, punctul rezultat s2 este conectat la polul planului de accelerație. Apoi.
Forța de inerție este aplicată în centrul masei S2 și este îndreptată în direcția opusă față de accelerarea centrului de masă (figura 16).
Pentru a găsi momentul inerției.
găsim accelerația unghiulară a liniei 2:
Pentru a determina direcția 2 transferăm vectorul tangențial component din planul de accelerare în planul mecanismului până la punctul C. Acest vector arată direcția # 949; 2; Min2 este îndreptat în direcția opusă.
Legătura 3 face mișcarea de translație în șinele rafturii. Inerția acestei legături se găsește ca:
și este îndreptată în direcția opusă față de as3. Mg3 = 0, deoarece # 949; 3 = 0.
1.5.3 Determinarea reacțiilor în perechile cinematice și forța de echilibrare a mecanismului de manivelă (Figura 18)
Cercetarea forțată a mecanismului este efectuată de grupurile Assur începând de la ultimul grup asirian, pentru care sunt cunoscute toate forțele externe, și finalizarea calculului luând în considerare legătura inițială pe care este necesară determinarea forței sau momentului de echilibrare.
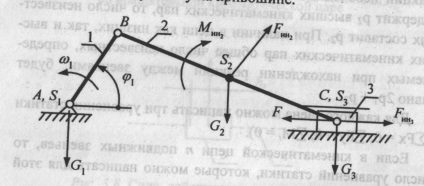
Fig. 18. Calculul puterii mecanismului glisorului
Fig. 19. Reacții care acționează asupra legăturilor din grupul de clasa a doua Assur, al doilea ordin, a doua specie
Fig. 20. Poligon de putere pentru determinarea reacțiilor care acționează asupra legăturilor grupului asyrian de tip 2
În calculele de forță, legătura pe care doriți să determinați Fyp sau Moore este considerată ca fiind prima legătură.
Legăturile 2 și 3 formează grupul structural Assurian de clasa a doua, de ordinul doi, de tip 2, pentru care este cunoscută forța exterioară F.
Reprezentăm grupul structural al legăturilor 2 -3 în aceeași poziție și la aceeași scară ca în schema mecanismului. Să arătăm reacțiile F21 și F30. care înlocuiesc acțiunea legăturilor aruncate 1 și 0 (figura 19).
Vom compila un tabel în care vom scrie secvența de determinare a reacțiilor, ecuațiile care trebuie compilate pentru a determina aceste reacții și numărul de legături pentru care sunt formulate aceste ecuații.
,
- Pentru a găsi u, compunem ecuația vectorilor de forțe:
Alegeți o scară pentru a construi un poligon de forță:
unde ab este un vector arbitrar reprezentând pe o scară.
Definim segmentele prin care forțele rămase vor fi extrase în scală:
După aceea, construim o închisă # 931; = 0), poligonul de forță (Figura 20) în secvența în care forțele sunt înregistrate, la determinarea # 931; . în urma căruia găsim vectori reprezentând reacțiile căutate. Valorile acestor reacții vor fi egale cu:
Reacția completă va fi compusă din componentele sale normale și tangențiale:
.
Mărimea forței va fi: [H].
Pentru a găsi reacția, vom compune ecuațiile vectoriale:
.
Primii patru vectori în conformitate cu ecuația (3) sunt deja construiți în Fig. Prin urmare, pentru a determina magnitudinea și direcția forței, conectăm originea vectorului la sfârșitul vectorului.
În funcție de tipul de antrenare, se determină fie forța de echilibrare Fyp. sau contrabalansarea momentului Moore.
În cadrul studiului, puteți presupune în mod condiționat punctul Fyp al punctului B și presupuneți că linia de acțiune a acestei forțe este perpendiculară pe pârghia AB.
Dacă legătura de pornire este condusă de un ambreiaj, Moore este determinată.
Varianta 1. Definiția Fyp (figura 21, a).