Forțele de inerție ale punctelor materiale ale legăturii pot fi reduse la una
punct și, prin urmare, sunt reprezentate de vectorul lor principal și de momentul principal al perechilor de forțe inerțiale.
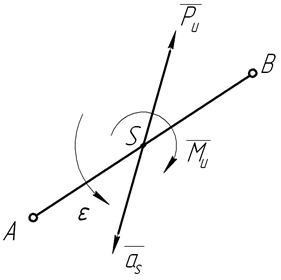
Fig.41 Încărcarea inerției în legătură
Principalul vector al forțelor de inerție, denumit de obicei forța de inerție a EV, este egal cu
unde m este greutatea legăturii, kg;
- accelerarea centrului S al masei de legătură, msec -2.
Direcția forței de inerție este opusă direcției vectorului și este măsurată în newtoni [H].
Să luăm în considerare cel mai general caz când legătura efectuează o mișcare paralelă plană. În acest caz, este recomandabil ca centrul de masă S (fig.41) să fie considerat punctul de reducere a forțelor de inerție ale legăturii, deoarece expresia momentului principal al perechii de forțe inerțiale (momentul inerțial) este simplificată. Acesta este definit ca
unde IS este momentul central al inerției legăturii față de axa care trece prin centrul său de masă S perpendicular pe planul mișcării sale, kgm 2;
[sec -2] este accelerarea unghiulară a legăturii, sec.
Momentul inerțial al MI este măsurat în Nm. Planul în care funcționează este paralel cu planul de mișcare al legăturii; este îndreptată în direcția opusă direcției - accelerația unghiulară a legăturii (Figura 40). Astfel, în cazurile de mai sus, sarcina inerțială a legăturii este reprezentată de forța inerțială. aplicată la punctul S și momentul inerțial.
Luăm în considerare câteva cazuri speciale.
Mișcarea progresivă a legăturii. Sarcina inerțială constă doar în forța inerțială = - m.
Rotirea legăturii în jurul centrului de masă cu accelerație unghiulară. Sarcina inerțială constă numai în momentul inerțial.
Rotirea legăturii în jurul centrului de masă. . Încărcarea inerțială a legăturii este absentă.
Determinarea forțelor inerțiale.
Pentru mecanismul de ghidare al compresorului (fig.42), găsiți sarcina inerțială a tuturor legăturilor, dacă lungimile legăturilor sunt 1AB = 0,05 m, lBC = 0,2 m; poziția centrelor de masă a legăturilor: S1 = A, lBS2 = 0,1 m, masa legăturilor: m1 = 0,2 kg, m2 = 0,5 kg, 3 m3 = 0,4 kg; momentul central al inerției barei de legătură VS-IS2 = 0,0018 kgm 2. Viteza unghiulară a manivelei AB este constantă și egală cu # 969; 1 = 80 secunde -1.
Problema este rezolvată pentru poziția mecanismului atunci când unghiul # 966; 1 = 45 °.
Soluția. 1) Am setat scara desenului # 956; l = 0,002 m / mm și se construiește o schemă a mecanismului (figura 42, a).
2) Construim un plan al vitezelor mecanismului (figura 42, b).
3) Construim planul accelerațiilor (fig.42, c).
4) Determinați sarcina inerțială pentru fiecare legătură a mecanismului.
a) Forțele inerțiale. Inerția manivelului este PI1 = 0, deoarece = 0. Forța de inerție a tijei de legătură este egală cu - m2 = - - m2 () A = 0.5 * 63 * 4 = 126 N. Aplicată în centrul masei sale S2 și în direcția opusă vectorului de accelerare a acestei legături (Figura 42, a). Forța de inerție a cursorului 3 este egală cu = - m3 = - m3 () (A se vedea punctul C = S3, figura 42, a) și în direcția opusă vectorului de accelerație al acestui centru.
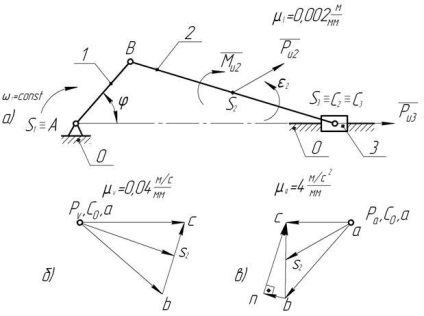
Fig. 42. Determinarea încărcăturii inerțiale a legăturilor mecanismului glisantei-manivelă.
a) un plan pentru poziția mecanismului; b) viteze plane; c) Planul de accelerare.
b) momentele inerțiale. Pentru o manivelă AV, momentul de inerție MI este
Mi1 = 0, deoarece legătura se rotește uniform ( # 949; 1 = 0).
Pentru tija de conectare, momentul inerțial MI2 se găsește după formula:
Acest moment este îndreptat opus accelerației unghiulare a legăturii de aeronavă (Figura 42, a).
Pentru cursorul 3, momentul inerțial MI3 este egal cu MI3 = 0, deoarece legătura se mișcă translațional (= 0).