Pentru a crea o histogramă, trebuie să definiți următorii parametri:
1. Puncte de frontieră.
2. În cazul nostru, punctele limită sunt valorile 162 și 190 (valorile minime și maxime din eșantion)
3. Numărul de clase de histograme este definit ca rădăcina pătrată a mărimii eșantionului.
În cazul nostru, dimensiunea eșantionului este egală cu șaisprezece, adică numărul de clase: sqrt (16) = 4
4. Lățimea unei clase: distanța dintre punctele de frontieră trebuie împărțită la numărul de clase.
În cazul nostru, lățimea unei clase este calculată ca (190-162) / 4 = 7
Acum trebuie să definim limitele fiecărei clase:
Clasa I: 162-168
Clasa a II-a: 169-175
Gradul 3: 176-182
Clasa a IV-a: 183-190
După ce am făcut-o <сетку> histograme pe sistemul de coordonate, este necesar să notăm numărul de evenimente din eșantionul nostru care intră în această clasă sau în acea clasă.
Histograma arată cât de des în eșantionul nostru apare o valoare sau o altă valoare.
3) Diagrama fluxului - afișarea grafică a secvenței de operațiuni într-un proces separat, indicând căi alternative de evenimente în cazul îndeplinirii sau neîndeplinirii anumitor condiții.
Fragmentul diagramei <Прием продукции на склад>.
4) Schema Ishikawa (diagrama cauză-efect) prezentată în Fig. 5, permite formalizarea și structurarea cauzelor apariției unui eveniment, de exemplu, apariția neconformității și, de asemenea, stabilirea relațiilor cauză-efect.
Toate cauzele posibile sunt clasificate conform principiului <5М>:
1. Omul (omul) - motive legate de factorul uman
2. Mașini (mașini, echipamente) - cauze legate de echipamente
3. Materiale - motive legate de materiale
4. Metode - motivele asociate cu tehnologia muncii, cu organizarea proceselor
5. Măsurători - motivele pentru metodele de măsurare.
Evenimentul investigat este afișat pe partea dreaptă a diagramei, simbolizând rădăcina diagramei arborescentă, care este construită în partea dreaptă a desemnării evenimentului. Pe orizontală, de la rădăcina diagramei până la marginea din stânga a foii, se aplică axa centrală a diagramei, similar cu trunchiul copacului. La axa centrală a diagramei lui K. Ishikawa sunt cinci ramuri, fiecare dintre ele corespund clasei sale de cauze sau proprii <М>.
Diagrama cauzală a lui K. Ishikawa
Mai mult, pe fiecare ramură separat, ca pe axă, suplimentar <веточки>, fiecare dintre acestea reprezentând o cauză separată în clasa sa. Pentru fiecare dintre acestea <веточке>, la rândul lor, sunt însumate lăstarile-cauze ale unui nivel mai înalt, care detaliază acest lucru. Continuând astfel, obținem un copac ramificat, legând cauzele apariției unui eveniment, la diferite nivele de detaliu. Astfel, putem stabili o relație de cauzalitate între abaterile individuale de la normă (cauzele primare) și influența lor asupra probabilității apariției unui anumit eveniment.
Pentru eficacitatea acestei metode și fiabilitatea rezultatelor obținute, construcția diagramei lui K. Ishikawa trebuie realizată de către profesioniști. Datorită structurii sale, diagrama lui Ishikawa este, de asemenea, numită <рыбья кость>.
5) Diagrama Pareto. sau analiza ABC, vă permite să identificați principalele cauze care au cel mai mare impact asupra apariției unei situații particulare. Principiul Pareto afirmă că 20% dintre cauze duc la 80% din consecințe. Cu alte cuvinte, din toate cauzele posibile, doar 20% sunt deosebit de semnificative, deoarece ele afectează rezultatele, care reprezintă 80% din total.
Principiul Pareto este încă numit <Правило 20-80>. Acest principiu este numit de economistul italian Wilfredo Pareto, care la sfârșitul secolului al XIX-lea a atras atenția asupra faptului că 80% din capitalul italian este concentrat în mâinile a 20% din populația Italiei. Mai târziu, validitatea acestei reguli a fost confirmată de observații și de constatările ulterioare ale rezultatelor în diverse ramuri ale vieții. Astfel, eliminarea a 20% din numărul total de neconcordanțe apare deturnarea a 80% din costul total al eliminării tuturor posibilelor neconcordanțe; pentru compania furnizoare, 20% din numărul total de clienți formează 80% din profit și așa mai departe. Astfel, prin concentrarea impactului asupra a 20% din cauze, avem un impact asupra a 80% din consecințe. Următoarele 30% din motive provoacă, cu destul de ciudatoare, doar 15% din consecințe și, în final, restul de 50% afectează numai 5% din consecințe (Figura 6). Astfel, ne putem distrage atenția și impactul, pe baza semnificației și eficacității rezultatelor.
De exemplu, dacă luați un text arbitrar și calculați de câte ori apare fiecare literă în ea, atunci este foarte probabil ca literele care reprezintă 20% din alfabet să reprezinte aproximativ 80% din întregul text.
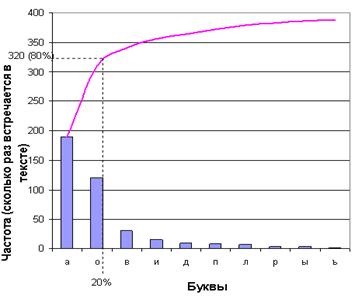
Diagrama lui V. Pareto
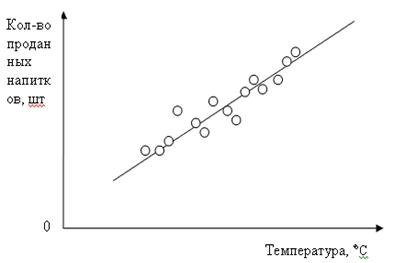
6) Diagrama de corelare (diagrama de dispersie) - reprezentarea grafică a relației dintre variabilele conectate una cu cealaltă. Cuvântul "corelare" înseamnă corelare, corespondență. Conexiunea, manifestată printr-un număr mare de observații sub forma unei relații definite între valoarea medie a atributului efectiv și factorii caracteristici, se numește corelație.
Diagrama de corelare este concepută pentru a detecta principiul prin care variabila dependentă condiționată se modifică pe măsură ce se modifică valoarea variabilei independente. De exemplu, cifra arată cum se modifică volumul vânzărilor de băuturi carbogazoase pe măsură ce condițiile meteorologice se schimbă. Există o puternică corelație pozitivă.
Coeficientul Fechner (coeficientul de corelare a semnalelor) este cel mai simplu indicator al etanșeității conexiunii. Se bazează pe o comparație a comportamentului deviației valorilor individuale ale fiecărei caracteristici (X și Y) față de valoarea medie. În acest caz, valorile abaterilor (Xi - X) și (Yi - Y) nu sunt luate în considerare. și semnele lor ("+" sau "-"). După determinarea semnelor de abatere de la valoarea medie în fiecare rând, sunt luate în considerare toate perechile de semne, iar numărul coincidențelor și discrepanțelor lor este contestat. Dacă coincidența semnelor este notată de C. și diferența este H., atunci coeficientul Fechner poate fi scris ca raportul dintre diferența dintre numărul de perechi de coincidențe și nepotrivirea semnelor la suma lor, adică la numărul total de unități observate:
Evident, dacă semnele tuturor abaterilor pentru fiecare caracteristică coincid, atunci ΣH = 0 și apoi K φ = 1. Aceasta caracterizează prezența unei conexiuni directe. Dacă toate semnele nu coincid, atunci ΣC = 0 și apoi K φ = -1 (feedback). Dacă ΣC = ΣH. atunci K = 0, nu există nicio conexiune. Astfel, ca orice indicator etanșeitate comunicare, raportul Fechner poate lua valori între 0 și ± 1. în acest caz, mai aproape de valoarea de 1, cu atât mai mare (mai puternică), în funcție de etanșeitate între X și Y. Pentru exemplul de mai sus K f = 0,8 .
Evaluarea paralelă a lui X și Y în n unități
Pentru aceasta, unitățile de observare sunt aranjate prin creșterea valorilor semnului de factor X și apoi comportamentul comportamentului valorilor caracteristicilor Y rezultante.
Ieșire X i
Costul producției nerealizate Y i