Editura Universității Federale din Orientul Îndepărtat
Scopul acestei lucrări este de a studia legile oscilațiilor unui pendul matematic și de a se familiariza cu tehnica determinării experimentale a accelerației gravitației cu ajutorul ei.
Scurtă teorie. Mișcarea mecanică a corpurilor este o schimbare a poziției lor în spațiu în timp. Mișcarea corpului este împărțită în trei tipuri:
traducere - toate punctele corpului se mișcă în același mod (viteza și accelerația tuturor punctelor corpului sunt aceleași atât în magnitudine cât și în direcție);
rotativ - toate punctele corpului se deplasează de-a lungul cercurilor în jurul unui centru sau axă comune;
vibrational - toate punctele corpului efectuează o mișcare alternativă sau înapoi și înapoi. Cu mișcare oscilantă liniară, punctul M nu depășește niciun segment KL al acestei linii și trece în mod repetat prin aceleași poziții din interiorul acestui segment (figura 1). Mișcarea mișcării este caracterizată printr-o anumită frecvență în timp. Dacă există un anumit interval de timp T într-o astfel de mișcare, prin care mișcarea punctului M este exact repetată, atunci o astfel de vibrație se numește o oscilație periodică.
Există multe tipuri diferite de oscilații periodice, dintre care cele mai simple sunt oscilațiile armonice - oscilațiile în care valoarea fizică (sau orice altă valoare) se modifică în timp într-o lege sinusoidală sau cosinusă. Oscilațiile armonice reprezintă o idealizare care ocupă un loc special printre toate celelalte fluctuații, care se datorează două motive:
1) oscilațiile întâlnite în natură și tehnologie au adesea un caracter apropiat de oscilații armonice;
2) orice fluctuație inharmonică poate fi reprezentată ca o sumă (impunere) a diferitelor oscilații armonice.
Ecuația cinematică a oscilațiilor armonice are forma
În ecuațiile (1) și (2):
X este deplasarea (abaterea) punctului oscilant din poziția de echilibru la momentul t;
A este amplitudinea oscilațiilor, aceasta este valoarea care determină abaterea maximă a punctului oscilant din poziția de echilibru (A = | Xmax |). Amplitudinea și polaritatea în sistemul SI sunt măsurate în metri.
ω este frecvența ciclică, o valoare care indică numărul de oscilații totale apărute în timpul a două secunde. În sistemul SI, frecvența ciclică este măsurată în s -1. Frecvența ciclică este legată de perioada oscilațiilor T și frecvența v.
T este perioada de oscilație. o cantitate care determină timpul unei singure oscilații (intervalul de timp dintre două treceri succesive ale punctului oscilant prin aceeași poziție în aceeași direcție). sau ω =. Perioada din sistemul SI este măsurată în câteva secunde.
v este frecvența oscilațiilor, o cantitate care indică numărul de oscilații totale pe unitate de timp. Frecvența este legată de perioada și de frecvența ciclică prin relațiile:. În sistemul SI, frecvența ν este măsurată în hertz (hertz este o oscilație pe secundă).
ωt + φ este faza oscilațiilor, o cantitate care determină cantitatea de deplasare X a punctului oscilant din poziția de echilibru la un moment dat t.
este etapa inițială. o cantitate care determină cantitatea deplasării X a punctului oscilant din poziția de echilibru în momentul inițial al timpului (t = 0). Faza inițială și faza oscilațiilor sunt măsurate în unități unghiulare, adică în grade sau în radiani (în fracțiuni de π).
Folosind una dintre ecuațiile cinematice ale oscilațiilor armonice, de exemplu, ecuația (1), găsim caracteristicile cinematice ale acestor oscilații - viteză și accelerare.
Viteza V este prima dată derivată a deplasării X:
V = AωCos (ωt +), (3)
unde Aω este amplitudinea vitezei Av a oscilațiilor armonice.
Accelerația oscilațiilor armonice α este definită ca prima derivare a vitezei oscilațiilor armonice sau a doua oară derivată a deplasării
α = = - Ao2Sin (ωt + f0), (4)
unde A ω2 este amplitudinea de accelerație Aα. Luând în considerare ecuația (1), accelerația oscilațiilor armonice (ecuația (4)) poate fi reprezentată într-o altă formă:
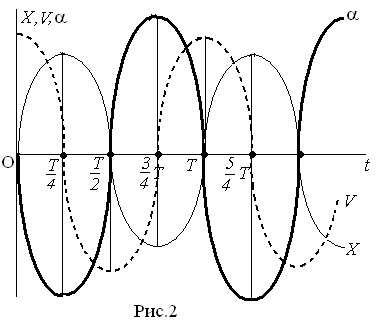
Se poate observa din formulele 1, 2 și 3 că, pentru oscilațiile armonice, deplasarea, viteza și accelerația sunt caracterizate de aceeași frecvență ciclică și, prin urmare, de perioada (T =). Fazele oscilațiilor acestor cantități sunt diferite: oscilația vitezei este înaintea oscilației deplasării fazei cu (în timp per), oscilația accelerației este înaintea deplasării deplasării fazelor cu π (în timp per).
Figura 2 prezintă curbele de timp, deplasare, viteză și accelerare (faza inițială este φ0 = 0). Așa cum se poate vedea din figură, în momentul în care poziția de echilibru (O = 0) trece prin punct, viteza sa este maximă. Atunci când punctul este deviat de la poziția de echilibru (X = + A sau X = -A), viteza sa este zero și accelerația devine maximă. În acest caz, semnul de accelerare este întotdeauna opus semnei de deplasare, adică accelerația este întotdeauna direcționată spre poziția de echilibru a punctului oscilant.
Cunoscând masa m a particulei instabile (punctul material) și accelerarea ei determinată de ecuația (5), găsim forța sub care se realizează oscilațiile armonice. Conform celei de-a doua legi a lui Newton, această forță este
unde k = mω2 - coeficientul de proporționalitate este o constantă pentru un anumit oscilator (oscilator - sistem fizic care efectuează vibrații). Se poate observa din ecuația (6) că forța care provoacă oscilația armonică este proporțională cu deplasarea X și este îndreptată împotriva deplasării, așa cum este indicat de semnul minus. Această forță tinde să readucă punctul de oscilație într-o poziție de echilibru, deci se numește forța de întoarcere. O astfel de forță, de exemplu, poate fi elasticitatea. apărută la mici deformări de orice fel, care, conform legii lui Hooke, este proporțională cu deformarea (deplasarea) ΔX și opusă acesteia în semn. Forțele de întoarcere pot avea un caracter diferit, nu elastic. În aceste cazuri, ele se numesc forțe cvasi-elastice (adică "asemănătoare forțelor elastice"). Coeficientul k. Determinarea valorii forței care determină deplasarea se numește coeficientul forței de refacere. Atât forțele elastice cât și forțele quasietice sunt forțe interne ale sistemului oscilant. În consecință, oscilațiile armonice apar sub acțiunea forțelor elastice interne sau similare, cvasi-elastice asupra lor. Oscilațiile care apar numai sub acțiunea forțelor interne sunt numite libere (sau proprii).
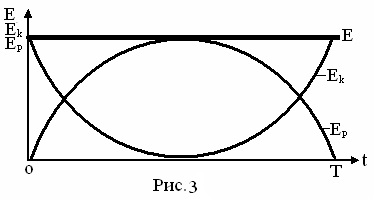
Energia oscilațiilor armonice. Pentru oscilațiile armonice se respectă legea conservării energiei mecanice, conform căreia energia totală E a oscilatorului armonic rămâne constantă. Să dovedim această afirmație. Energia mecanică totală E constă în energia kinetică Ek și energia potențială Ep
Energia cinetică este o măsură a mișcării și pentru un punct material (sau mișcarea de translație a unui corp solid) este determinată de formula
unde m este masa punctului oscilant și V este viteza mișcării sale.
Energia potențială este determinată de starea corpului sau de poziția sa în spațiu. Pentru forțele elastice (sau cvasi-elastice), energia potențială a unui corp este determinată de formula
unde k este coeficientul de elasticitate, X este deplasarea punctului oscilant din poziția de echilibru.
expresie pentru energia mecanică totală a oscilațiilor armonice:
Cantitățile din ecuația din dreapta (k și A) sunt constante pentru un anumit oscilator armonic și, prin urmare, energia totală a oscilațiilor armonice E pentru un oscilator dat este constantă. În acest caz, ambele energii cinetice și potențiale se schimbă în antifază, respectiv, conform legilor patratice ale cosinusului și sinusului (Figura 3).
Pendulul matematic, perioada oscilațiilor sale. Un exemplu de oscilații armonice mecanice sub acțiunea forțelor cvasi-elastice este oscilația unui pendul matematic. Un pendul matematic se numește un sistem idealizat constând dintr-un fir fără greutate și inextensibil, pe care se suspendă o masă concentrată la un punct. O aproximație destul de bună față de un pendul matematic este o mică minge greu suspendată pe un fir lung, subțire, ne-întins (fig.4). Două forțe acționează întotdeauna asupra mingii pendulului: forța gravitației și tensiunea firului. În poziția de echilibru (un pendul suspendat liber), suma acestor forțe este zero. Pe bilele pendulului, se abate de la poziția de echilibru la unghiul φ. forța de refacere egală cu rezultatul celor două forțe va acționa: gravitatea (accelerația gravitației) și forța de tensionare a firului.
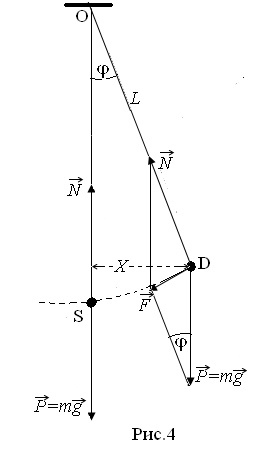
Sub acțiunea acestei forțe de refacere, pendulul va începe să se miște rapid de la punctul D la punctul S (poziția de echilibru). La punctul S, forța este zero, dar din moment ce pendulul are o masă m și la momentul trecerii punctului S are viteza V, el va trece acest punct prin inerție. Cu mișcarea suplimentară a pendulului de-a lungul arcului, viteza sa va scădea deoarece direcția forței se schimbă și va fi opusă direcției de mișcare a pendulului. În punctul final al mișcării, pendulul se oprește și începe imediat să se deplaseze în punctul S. Astfel, pendulul va efectua mișcări vibraționale sub acțiunea forței. Dacă forța de frecare nu acționează asupra pendulului, atunci va efectua mișcări oscilante pentru un timp infinit de lung. Se poate vedea din figura 4 că magnitudinea forței este legată de magnitudinea gravitației prin relația:
Dependența forței de restabilire de deplasare, caracterizată prin unghiul φ, în ecuația (11), este neliniară, prin urmare, oscilațiile pendulului nu vor fi armonice. Cu toate acestea, în cazul oscilațiilor mici ale pendulului, atunci când unghiul de deformare φ este atât de mic (până la 5 °), Snφ = ≈ φ. forța de refacere este proporțională cu unghiul φ și în acest caz (pentru mici deviații) putem presupune că oscilațiile pendulului apar sub acțiunea unei forțe cvasi-elastice și, prin urmare, oscilațiile sunt armonice. Unghiurile mici de abatere φ corespund unei mici valori a deplasării X. Se substituie în (11) în loc de Syn. și luând în considerare faptul că pentru unghiuri mici de abatere φ. vectorul de forță va coincide practic cu segmentul de deplasare X, dar este direcționat opus deflecției, în cele din urmă este posibil să se scrie forța de întoarcere (cvasi-elastică) sub forma
Prin urmare, pentru unghiuri de abatere mici φ. Forța cvasi-elastică va acționa asupra pendulului și va efectua oscilații armonice. Să găsim perioada unor astfel de oscilații armonice ale unui pendul matematic. Pentru a face acest lucru, vom scrie a doua lege a lui Newton în formă scalară:
unde α = este accelerarea mingii oscilante a pendulului matematic, După redusarea masei în ecuația (13), obținem ecuația în forma: = - sau
Deoarece în aceste ecuații cantitățile g și L sunt întotdeauna pozitive, raportul lor poate fi egal cu pătratul unei anumite valori ω 2: