Transformările clasice galileene sunt incompatibile cu postulatele SRT și, prin urmare, trebuie înlocuite. Aceste noi conversie trebuie să stabilească o legătură între coordonatele (xy z) și timp punct t evenimentele observate în cadrul K. și coordonatele (x „Y“. Z «) și timpul t» a acelorași evenimente observate pe referința sistemului K “.
Formulele cinematice pentru transformarea coordonatelor și a timpului în SRT sunt numite transformările Lorentz. Acestea au fost propuse în 1904 chiar înainte de apariția SRT ca transformări, în legătură cu care ecuațiile de electrodinamică sunt invariabile. Pentru cazul în care sistemul K 'se deplasează în raport cu K cu viteza υ de-a lungul axei x. transformările Lorentz au forma:
O serie întreagă de consecințe rezultă din transformările lui Lorentz. În special, efectul relativist de întârziere a timpului și contracția Lorentz a lungimii rezultă din ele. Să presupunem, de exemplu, la un anumit „sistem K“ x punct este durata procesului τ0 = t'2 - t'1 (ora intern), unde t'1 și t'2 - ceasul din sistemul K „la începutul și sfârșitul procesului. Durata τ a acestui proces în sistemul K va fi egală cu
În mod similar, se poate demonstra că scurtarea relativistă a lungimii rezultă din transformările lui Lorentz. Una dintre cele mai importante consecințe ale transformărilor Lorentz este concluzia despre relativitatea simultană. Să presupunem, de exemplu, că două evenimente apar simultan în două puncte diferite ale cadrului de referință K '(x'1 ≠ x'2) din punctul de vedere al observatorului în K' (t'1 = t'2 = t '). Conform transformărilor Lorentz, observatorul din sistemul K va avea
În consecință, în sistemul K aceste evenimente rămân spațiale disociate. se dovedește a fi non-simultană. Mai mult decât atât, diferența t2 semn - t1 determinată de semnul expresiei υ (x'2 - x'1), cu toate acestea, în unele cadre pot precede primul eveniment la a doua, în timp ce în alte sisteme de referință, dimpotrivă, al doilea eveniment precede primul. Această concluzie a SRT nu se aplică evenimentelor legate de relația cauză-efect. când unul dintre evenimente este consecința fizică a celuilalt. Se poate arăta că SRT nu încalcă principiul cauzalității. iar ordinea evenimentelor cauzale este aceeași în toate formele de referință inerțiale.
Relativitatea simultană a evenimentelor separate prin spațiu poate fi ilustrată prin exemplul următor.
Să presupunem că în cadrul de referință K 'de-a lungul axei x' o bară rigidă lungă este localizată în mod imobiliar. În centrul tijei se află lampa blițului B., iar la capete sunt două ceasuri sincronizate (figura 4.4.1 (a)), sistemul K 'se deplasează de-a lungul axei x a sistemului K la o viteză υ. La un moment dat, lampa trimite impulsuri scurte de lumină spre capetele tijei. Datorită egalității ambelor direcții, lumina din sistemul K 'va ajunge simultan la capetele tijei, iar ceasurile fixate la capetele tijei vor afișa același timp t'. În ceea ce privește sistemul K, capetele tijei se mișcă cu viteza υ, astfel încât un capăt să se îndrepte spre pulsul luminii, iar celălalt capăt al luminii trebuie să se prindă. Deoarece vitezele de propagare ale impulsurilor luminoase în ambele direcții sunt aceleași și egale cu c. atunci, din punctul de vedere al observatorului din sistemul K, lumina va ajunge la capătul stâng al tijei mai devreme decât cel din dreapta (Figura 4.4.1 (b)).
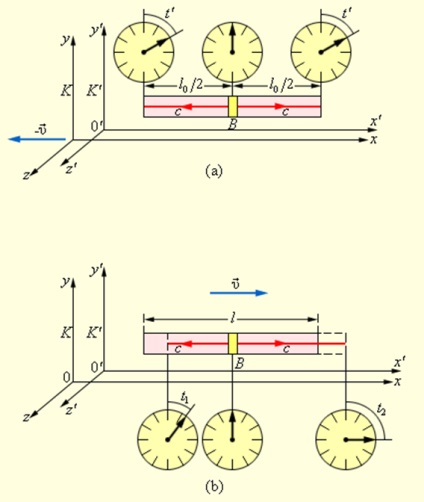
Relativitatea simultană. Pulsul luminos ajunge la capetele tijei solide simultan în cadrul de referință K '(a) și nu simultan în cadrul de referință K (b)
Transformările Lorentz exprimă natura relativă a intervalelor de timp și distanță. Cu toate acestea, în SRT, împreună cu afirmația naturii relative a spațiului și a timpului, un rol important îl are stabilirea unor cantități fizice invariabile care nu se schimbă în timpul tranziției de la un cadru de referință la altul. O astfel de cantitate este viteza luminii într-un vid c. care în STR devine absolută. O altă cantitate invariantă importantă, care reflectă natura absolută a relațiilor spațiu-timp, este intervalul dintre evenimente.
Intervalul spațiu-oră este definit în SRT prin următoarea relație:
unde t12 este intervalul de timp dintre evenimentele dintr-un anumit cadru de referință și l12 este distanța dintre punctele la care evenimentele luate în considerare apar în același cadru de referință. În cazul particular, când unul dintre evenimente are loc la originea (x1 = y1 = z1 = 0) a cadrului de referință la momentul t1 = 0, iar al doilea în punctul cu coordonatele x. y. z la ora t. Intervalul spațiu-oră dintre aceste evenimente este scris în formular
Cu ajutorul transformărilor Lorentz se poate arăta că intervalul spațiu-timp între două evenimente nu se schimbă în timpul trecerii de la un sistem inerțial la altul. Invarianța intervalului înseamnă că, în ciuda relativității distanțelor și a intervalelor de timp, cursul proceselor fizice este de natură obiectivă și nu depinde de cadrul de referință.
Dacă unul dintre evenimente este un fulger de lumină la originea cadrului de referință la t = 0, iar al doilea este sosirea frontului luminii la punctul cu coordonatele x. y. z la momentul t (Figura 4.1.3), atunci
și, în consecință, intervalul pentru această pereche de evenimente s = 0. Într-un alt sistem de referință, coordonatele și timpul celui de-al doilea eveniment vor fi diferite, dar în acest sistem intervalul spațiu-timp s 'va fi zero,
Pentru oricare două evenimente conectate printr-un semnal luminos, intervalul este zero.
Din transformările Lorentz pentru coordonate și timp, se poate obține legea relativistă de adăugare a vitezelor. Fie, de exemplu, în cadrul referinței K 'de-a lungul axei x' particula se mișcă cu viteză. Componentele vitezei particulei u'x și u'z sunt egale cu zero. Viteza acestei particule în sistemul K va fi egală cu
Folosind operația de diferențiere de la formulele de transformare Lorentz se găsesc:
Aceste relații exprimă legea relativistă de adăugare a vitezelor pentru cazul în care particula se mișcă paralel cu viteza relativă a cadrelor de referință K și K '.
Pentru υ < Dacă în sistemul K 'de-a lungul axei x cu o viteză u'x = c se propagă impulsul luminos, apoi pentru viteza ux a impulsului în sistemul K obținem Astfel, în cadrul de referință K, pulsul luminos se propagă de-a lungul axei x la o viteză c. care este de acord cu postulatul invarianței vitezei luminii.Articole similare