În orice moment în planul figurii, cu mișcarea plată neschimbată, există un singur punct a cărui viteză este zero. Acest punct este numit centrul de viteze instantanee (MSC).
Fie ca viteza punctului A al planului să fie cunoscută și egală cu
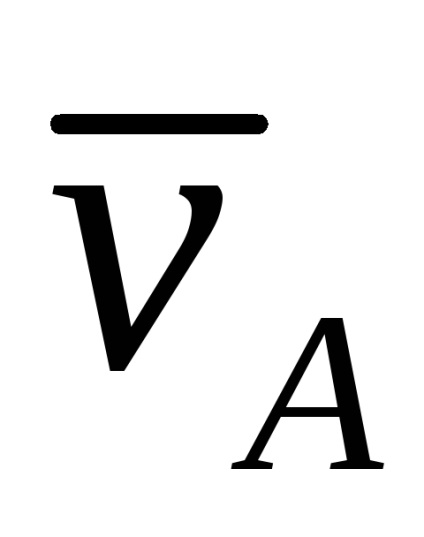
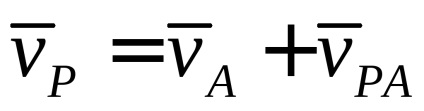
Vom căuta poziția unui punct la care viteza la un moment dat este zero. prin urmare
.
Din proprietățile produsului vectoric rezultă vectorul


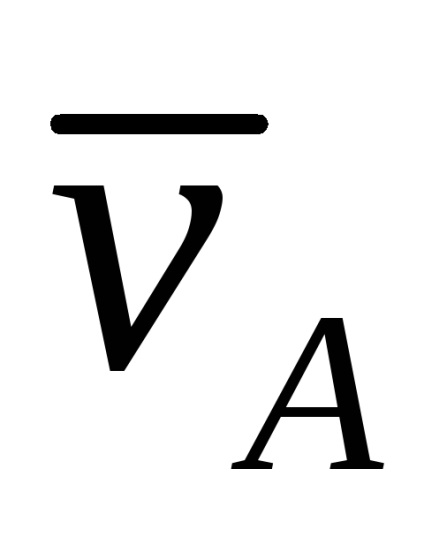
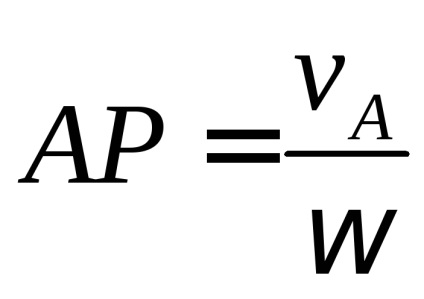
Punctul "P" găsit în acest fel este centrul instantaneu al vitezelor.
Fig. 1. Centrul vitezei instantanee
Evident, dacă luăm celălalt punct al unei figuri plane ca pol, să presupunem punctul C, apoi, după cum sa dovedit mai sus, MSC. ar trebui să fie pe perpendicularul tras de la punctul C la viteza acestui punct (Fig.1.13). Astfel, MSC. este punctul de intersecție a perpendicularilor la vitezele punctelor planului.
Dacă acum luăm punctul P ca pol, atunci viteza de transport a oricărui alt punct va fi zero. Apoi, viteza absolută a unui punct arbitrar al unei figuri plane va fi egală cu viteza sa în mișcarea de rotație din jurul MSC.
Cunoscând poziția MSC și viteza unghiulară a figurii plane, puteți determina viteza oricărui punct la un moment dat și puteți determina viteza punctului corpului rotativ. După cum sa menționat deja, MSC este definită pentru o poziție dată a unei figuri plate. În poziția adiacentă, centrul de viteză instantanee este un alt punct.
Proprietățile centrului de viteză instantanee:
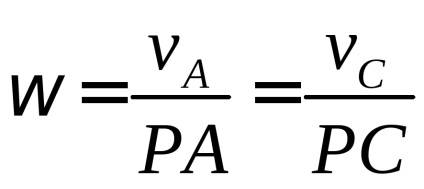
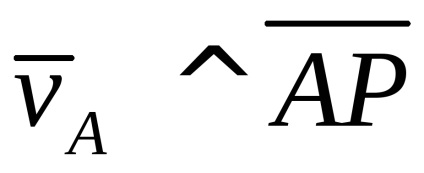

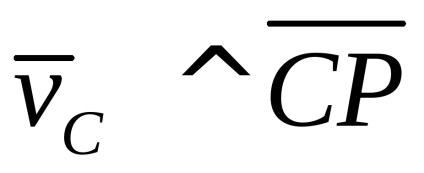

Exemple de definiție a msc.
Atunci când se rotește o roată cu rază pe o suprafață aspră fără alunecare, MSC se află în punctul de contact al roții cu o suprafață fixă
Dacă vitezele a două puncte ale unei figuri plane sunt paralele, dar nu egale unele cu altele, atunci (vezi Fig.1.14 a, c)
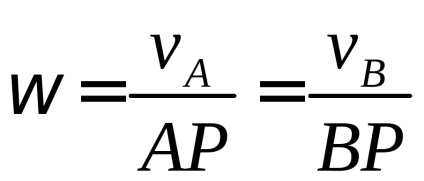
Fig. 1. 14. Vitezele punctelor în mișcarea plană a unui corp rigid
În cazul egalității vitezelor paralele (vezi Fig.1.14 b) MDC. este în infinit.
Viteza unghiulară a cifrei este zero în acest caz. Vitezele tuturor punctelor sunt egale. Se spune că cifra efectuează o mișcare de translație instantanee la momentul de timp, care diferă de mișcarea de translație prin faptul că accelerațiile diferitelor puncte nu sunt neapărat egale:
Dacă vitezele a două puncte sunt antiparalerale, atunci (vezi Fig.1.14 c)
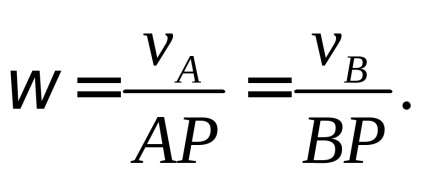
Teorema privind accelerarea punctelor unei figuri plane
Accelerația unui punct, implicat în mișcarea plană a unui corp rigid poate fi definit ca suma unui pol de accelerare geometrică și accelerația punctului în mișcarea de rotație în jurul stâlpului.
Pentru a demonstra această propoziție, vom folosi teorema privind adăugarea de accelerații a punctului în mișcarea compusului. Luăm punct

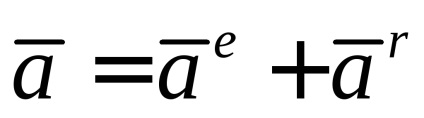
pentru că în mișcarea înainte a accelerației tuturor punctelor sunt aceleași și egale cu accelerația polului, avem
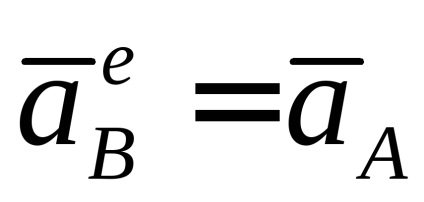
Accelerarea punctului în timpul mișcării de-a lungul circumferinței este convenabilă pentru a reprezenta suma componentelor centripetale și rotative:
.
.
Direcțiile componentelor accelerației
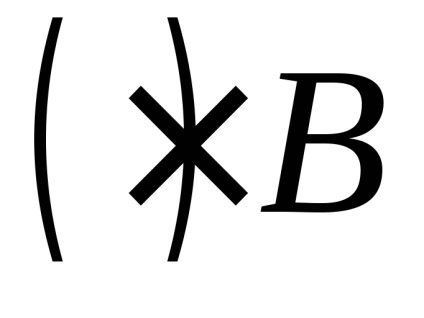
Componenta normală (centripetală) a accelerației relative este determinată de formula
Valoarea lui este
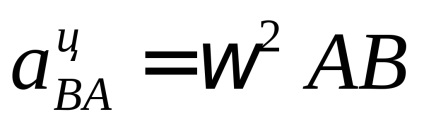
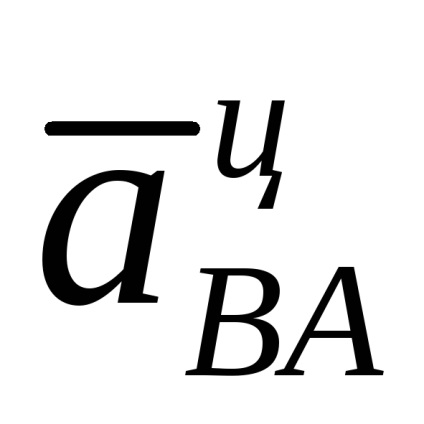
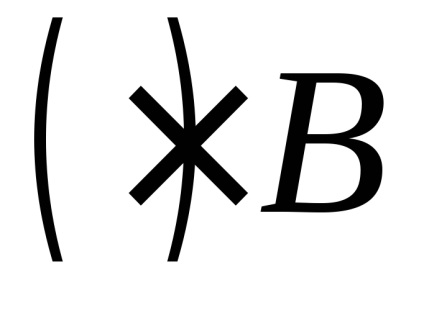
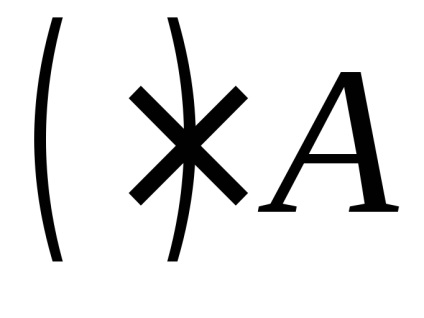
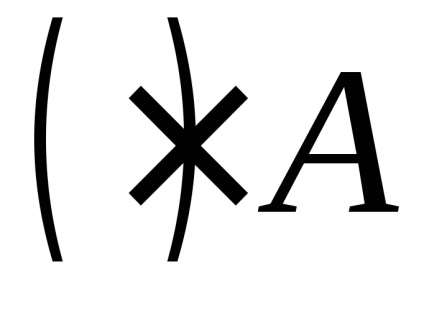
Fig. 1. Teorema privind adăugarea accelerărilor (a) a consecințelor sale (b)
Componenta tangențială (rotativă) a accelerației relative este dată de
.
Modulul acestei accelerații se găsește prin accelerația unghiulară
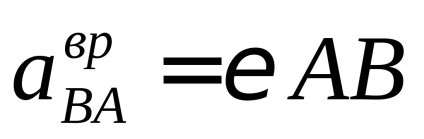
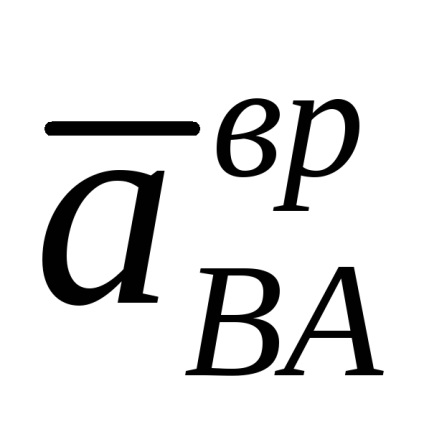
Amplitudinea accelerației relative totale este determinată de teorema lui Pitagora:
.
Vectorul de accelerație relativă a oricărui punct al planului este deviat de linia dreaptă care leagă punctul considerat cu polul printr-un unghi

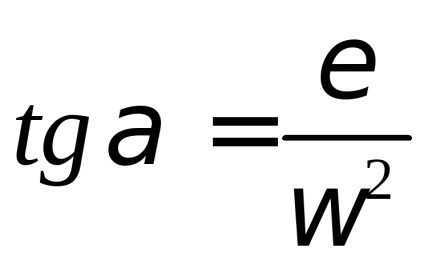
Figura 1.15 b arată că acest unghi este același pentru toate punctele corpului.
Corolarul teoremei privind accelerațiile.
Capetele vectorilor de accelerație ale punctelor segmentului rectiliniu pe planul planului se află pe o linie și o împart în părți proporționale cu distanțele dintre puncte.
Dovada acestei declarații rezultă din figură:
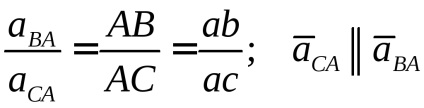
Metodele de determinare a accelerației punctelor unui corp cu mișcarea plană sunt identice cu metodele corespunzătoare pentru determinarea vitezelor.