Două avioane se intersectează într-o linie dreaptă, pentru construcția căreia este necesar să se determine două puncte care aparțin simultan ambelor planuri (Figura 3.1). În figura 3.1, linia de intersecție MN a ABCD-ului patrulater cu triunghiul EFK este construită și se determină vizibilitatea părților sale.
Principala metodă de rezolvare a problemei este de a stabili punctele de intersecție a două laturi ale unei figuri cu planul celei de-a doua figuri și de a le conecta împreună. Problema este redusă la rezolvarea problemei construirii punctului de intersecție al unei linii drepte cu un avion.
Considerăm partea EK a triunghiului EFK drept linie (e 'k', ek) și găsim punctul de întâlnire M (m ', m) cu paralelogram ABCD.
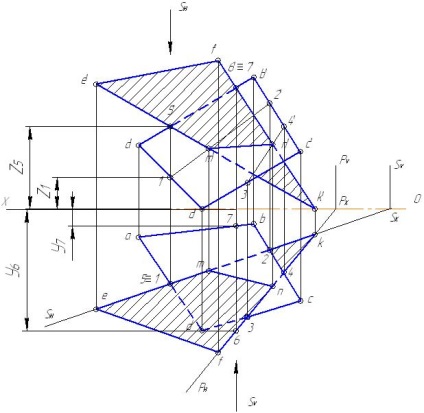
Figura 3.1 - Intersecția figurilor plate
Algoritmul pentru această sarcină este după cum urmează:
- închidem partea EK în planul auxiliar de proiectare orizontală S (EK Î S. S ^ H.SH Î ek);
- planul S intersectează planul ABCD quadrilateral de-a lungul liniei drepte I-II (1'-2 ', 1-2). Se marchează proiecțiile orizontale de 1, 2 puncte de intersecție a laturilor EK și FK cu planul S. Apoi de-a lungul liniei de legătură găsim proiecțiile lor frontale - punctele 1 'și 2' [S ∩ ABCD ð I-II (1'-2 ', 1-2)];
- planul S intersectează de asemenea planul triunghiului EFK de-a lungul liniei EK (e 'k', ek). În planul orizontal al proiecției, linia ek coincide cu traiectoria orizontală a SH. și pe proiecția frontală plană intersecția liniilor de proiecție față 1'-2 „și e“ k „ne oferă o proiecție m față“, iar pe orizontală de proiecție m găsi punctul necunoscut M [S ∩ ABCD ð EK (e 'k', ek), 1'-2 '∩ e' k 'ð m '→ m].
Definim cel de-al doilea punct comun N (n 'n), care aparține figurilor planului nostru și, prin urmare, liniile lor de intersecție. Pentru a face acest lucru, definim punctul de întâlnire al laturii triunghiului FK cu planul paralelogramului ABCD. Algoritmul soluției este același:
- încheiem partea FK în planul auxiliar de proiectare orizontală P (P ^ N. PH Î fk);
- a determina linia de intersecție III-IV (3'-4 ', 3-4) a planului P cu planul ABCD-ului patrulaterar;
- la intersecția proeminențelor frontale 3'-4 'și e' f 'marcăm proiecția frontală n', și de-a lungul ei găsim proiecția orizontală n a punctului căutat N.
Prin combinarea proiecțiilor cu aceleași nume M (m 'm) și N (n' n) unul cu celălalt, obținem linia necesară MN (m 'n', mn) a intersecției figurilor plane date.
Problema ar putea fi rezolvată prin luarea în considerație a oricărei părți a ABCD-ului patrulater ca linii și găsirea punctelor întâlnirii lor cu planul triunghiului EFK. sau considerați ca o linie o latură a unui triunghi și a unei părți a paralelogramului.
Planurile auxiliare pot fi executate atât pe orizontală, cât și pe proeminență. Rezultatul, desigur, nu se va schimba de la asta.
Vizibilitatea relativă a avioanelor este determinată de vizibilitatea liniilor drepte care îi aparțin. Linia de intersecție MN este linia de vedere.
Pentru a determina vizibilitatea pe diagrama, este necesar să ne amintim că atunci când se proiectează un obiect situat între observator și planul de proiecție, și că proiecția orizontală - este o vedere în plan și partea din față - vedere frontală.
Pentru a determina vizibilitatea, se utilizează metoda punctelor concurente. Punctele concurente sunt o pereche de puncte situate pe două linii intersectate și pe una perpendiculară (proeminentă) spre planul proiecțiilor.
Vizibilitatea pe planul orizontal al proiecției. Pe planul H ne uităm la SH săgeată și selectați proiecția orizontală a punctelor concurente de 5 și 1, situată pe liniile de răsucire ale CE. AD și unul perpendicular pe orizontală puncte de proiecție plane H. coincide 5 ≡ 1, dar proiecția frontală 5 „și 1“ sunt la distanțe diferite față de planul menționat H. Z5> Z1. și anume în spațiu, punctul 5 este situat mai sus decât punctul 1, prin urmare, de sus, vom vedea punctul 5, iar punctul 1 va fi închis. Punctul 5 de pe partea EK. înseamnă că această parte și o parte a figurii EFK vor fi vizibile pe proiecția orizontală. aparținând acestei părți. La punctele de m și n liniile de vizibilitate intersecție variază, și o porțiune de 1-d -3-m-N ABCD patrulater pe planul H va fi invizibil.
Vizibilitatea pe planul frontal al proiecției V. În planul V, uitați-vă la săgeata SV. și alegeți proiecțiile frontale ale punctelor 6 și 7 care se află pe liniile intersectate FK și AB. Acestea sunt situate pe un plan perpendicular pe proiecția V. Partea frontală a acestor puncte coincid 6 „≡ 7“, dar amplasarea proiecțiilor orizontale ale punctelor 6 și 7 permit să se stabilească care dintre aceste puncte sunt distanțate mai departe de planul V. adică este mai aproape de observator. În exemplul examinat, Y6> Y7. prin urmare, pe proiecția frontală, punctul 6 și partea FK sunt vizibile. pe care se află acest punct. Parte a triunghiului EFK. adiacent la partea FK. este situat deasupra și închide o parte a figurii ABCD-ului patrulateral. La punctele m 'și n', vizibilitatea este inversată.