Instrucțiuni. Pentru a obține o soluție, introduceți funcțiile în formatul y = f1 (x); y = f2 (x).
Este de asemenea convenabil să construiți o grafică folosind acest serviciu.
Exemplul №1. Calculați aria figurului delimitată de linii și x + y = 6.
Soluția. Să construim aceste linii în sistemul de coordonate xOy. Să găsim punctele de intersecție ale acestor linii
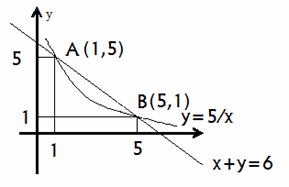
Fig.1. Pătrat al figurii.
Indicați aceste puncte cu A și B. Astfel, A (1; S), B (S; 1). Zona de căutare S este egală cu diferența dintre pătrate ale figurii delimitate de liniile x = 1, x = 5, y = 0, y = 6-x (notat zona prin S1), iar liniile x = 1, x = 5, y = 0, (aceasta desemnează zona cu S2). În acest fel
S = S1-S2
Zona S2 poate fi calculată utilizând un integral integrat
unități 2.
Zona S1 poate fi calculată ca sumă a suprafețelor unui triunghi dreptunghiular și a unui dreptunghi, dar este mai convenabil să se calculeze S1 ca un integral
.
Acum putem calcula suprafața necesară
S = S1 - S2 = 12-5 ln5
Răspuns: S = 12 - 5 ln5 unități 2.
Regulile de introducere a datelor
Adresați-vă întrebările sau lăsați-vă dorințele sau comentariile în partea de jos a paginii în secțiunea Disqus.
De asemenea, puteți lăsa o solicitare de ajutor în rezolvarea activității de control cu partenerii noștri de încredere (aici sau aici).