§ 93. Momentul rotativ al motorului asincron
Cuplul unui motor asincron este creat prin interacțiunea câmpului magnetic rotativ al statorului cu curenții din conductoarele înfășurării rotorului. Prin urmare, cuplul depinde atât de fluxul magnetic al statorului Ft. și pe curentul în bobina rotorului I2. Cu toate acestea, la crearea cuplului, participă numai energia activă consumată de mașină din rețea. Ca urmare, cuplul nu depinde de curentul din bobina rotorului I2, ci numai de componenta sa activă, adică I2 cos # 968; 2, unde Unghiul 2 faze între e. etc cu. și curentul în bobina rotorului.
Astfel, cuplul unui motor asincron este determinat de următoarea expresie:
unde C este constanta constructivă a mașinii, în funcție de numărul polilor și fazelor sale, numărul de înfășurări ale înfășurării statorului, designul structurii înfășurării și sistemul adoptat de unități. Cu condiția ca tensiunea aplicată să fie constantă, fluxul magnetic rămâne, de asemenea, aproape constant pentru orice schimbare a sarcinii motorului.
Astfel, în expresia cuplului, cantitățile C și Ft sunt constante, iar cuplul este proporțional doar cu componenta activă a curentului în bobina rotorului, adică,
Schimbarea sarcinii sau a cuplului de frânare pe arborele motorului modifică atât viteza de rotație a rotorului, cât și alunecarea.
Schimbarea alunecării provoacă o schimbare atât în puterea curentă în rotorul I2, cât și în componenta sa activă I2 cos # 968; 2 /
Este posibil să se determine curentul în rotor cu raportul e. etc cu. la rezistența totală, adică,
unde Z2, r2 și X2 reprezintă rezistența totală, activă și reactivă a fazei de înfășurare a rotorului.
Modificarea alunecării modifică frecvența curentului rotorului. Atunci când rotorul non-mobil (n2 = 0 și S = 1) câmp rotativ cu aceeași microfonie viteză intersectează conductorii înfășurările statorului și rotor și rotorul frecvența curentă este egală cu frecvența curentă a rețelei (f2 = f1). Când reducerea alunecarea de lichidare de câmpul magnetic al rotorului intersectează cu frecvența mai mică, astfel încât frecvența curentului în rotor-Micșorați cute. Atunci când rotorul se rotește sincron cu câmpul (n2 = n1 și S = 0), conductoarele înfășurarea rotorului nu intersectează câmpul magnetic, astfel încât frecvența curentului în rotor este zero = 0 f2. Astfel, frecvența curentului în rotor este proporțională cu alunecarea, adică f2 = Sf1
Rezistența activă a înfășurării rotorului este aproape independentă de frecvență, în timp ce e. dc și reactanță sunt proporționale cu frecvența, adică modifică cu o schimbare în alunecare și pot fi determinate de următoarele expresii:
unde E și X sunt e. etc cu. și rezistența inductivă a fazei de înfășurare a rotorului fix, respectiv.
Astfel, avem:
și cuplul
În consecință, pentru alunecare mici (aproximativ 20%) în cazul în care SX este mică în comparație cu r2, creșterea alunecare determină o creștere a cuplului, deoarece acest cărucior, se va topi componenta activă a curentului în Rotok (I2sos # 968; 2). Pentru diapozitivele mari (SX mai mari decât r2), o creștere a alunecării va cauza o scădere a cuplului. Astfel, pentru alunecare mare, creșterea sa, deși crește curentul în rotorul I2, dar componenta sa activă I2 cos În consecință, cuplul este redus ca urmare a unei creșteri semnificative a soiei reactive a rezistenței înfășurării rotorului.
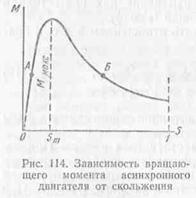
În Fig. 114 arată dependența cuplului la alunecare. Cu o ușoară alunecare de St (aproximativ 20%), motorul dezvoltă cuplul maxim care determină capacitatea de suprasarcină a motorului și este de obicei de 2-3 ori cuplul nominal.
Operarea constantă a motorului este posibilă numai pe ramura ascendentă a curbei dependenței momentului de alunecare, adică atunci când alunecarea variază de la 0 la Lucrarea motorului pe ramificația descendentă a dependenței indicate, adică cu alunecarea S> St. este imposibilă, deoarece nu există un echilibru stabil al momentelor.
Presupunând că cuplul este egal cu frânare Termen (MBP = Mtorm) la punctele A și B, apoi la momente aleatorii aborda echilibru într-un singur caz este redusă, iar celălalt nu este restabilită. Să presupunem că cuplul motorului a scăzut din anumite motive (de exemplu, atunci când tensiunea de rețea scade), atunci alunecarea va începe să crească. Dacă punctele de echilibru au fost la punctul A, creșterea alunecare va determina o creștere a cuplului motor și va deveni din nou egală cu cuplul de frână, T. E. Boc-moment, echilibrul devine. În cazul în care soldul momente a fost la punctul B, creșterea alunecare va determina o scădere a cuplului, care va rămâne întotdeauna mai puțin de frânare, de ex., E. echilibru momente este restabilit, iar viteza rotorului este redusă în mod continuu la oprire a motorului.
Dacă un cuplu de frânare mai mare decât cuplul maxim este aplicat pe arborele motorului, echilibrul dintre momente nu va fi restabilit și rotorul motorului se va opri.
Cuplul de rotație al motorului este proporțional cu pătratul tensiunii aplicate, deoarece atât fluxul magnetic, cât și curentul din rotor sunt proporționale cu tensiunea. Prin urmare, o schimbare a tensiunii în rețea generează o schimbare semnificativă a cuplului.
§ 94. CARACTERISTICI DE FUNCTIONARE ALE MOTORULUI ASINCRONUS
Caracteristicile de performanță a unui motor asincron sunt dependințele de alunecare S, viteza rotorului n2, cuplul de dezvoltare M, consumul de curent I1, consumul de putere P1, factorul de putere cos # 61546; și eficiența d. # 951; de la puterea utilă P2 pe arborele mașinii. Aceste caracteristici (Fig. 115) sunt îndepărtate trei condiții de funcționare a motorului natural, adică. E. Motor nereglementată, f1 frecvența și tensiunii U1 se whith rămân constante, iar schimbările numai sarcina pe arborele motorului.
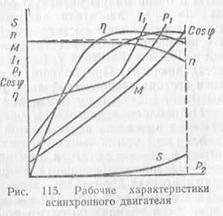
Cu o sarcină crescândă pe arborele motorului, alunecarea va crește, iar în cazul încărcăturilor mari, alunecarea crește oarecum mai repede decât la sarcini mici.
Când motorul este în gol, n2 = n1 sau S = 0.
La sarcina nominală, alunecarea este de obicei S = 3-5%.
Viteza rotorului
Ca și în cazul creșterii sarcinii pe arborele motorului, glisarea crește, atunci numărul de rotații va scădea. Cu toate acestea, modificarea vitezei de rotație cu sarcină crescătoare de la 0 la cea nominală este foarte ușoară și nu depășește 5%. De aceea, viteza caracteristică a unui motor asincron este rigidă - are o înclinare foarte mică față de axa orizontală.
Cuplul de rotație dezvoltat de motorul M este echilibrat de cuplul de frânare pe arborele M2 și de momentul în care depășesc pierderile mecanice M0,
unde P2 este puterea utilă a motorului,
# 2 - viteza unghiulară a rotorului.
Când motorul este în mișcare în gol, cuplul este M0; cu creșterea sarcinii pe arbore, acest moment crește și datorită unei anumite scăderi a vitezei rotorului, creșterea cuplului are loc mai repede decât creșterea puterii utile pe arbore.