Și acum imaginați-vă următoarea situație destul de plauzibilă: soția sa nu-i plăcea ideea de a face coloane în mijloc (ilustrate în figura 293.1 cu o culoare verde închis). Vrea spațiu și aerisire.
Nimic de făcut, femeile cunosc mai bine, bine, ne-a păstra acest lucru foarte lejeritate, au în plus pentru a calcula forma dreptunghiulara agricole (Figura 293.1 cu privire la liniile generale ale fermelor dreptunghiulare sunt prezentate în violet).
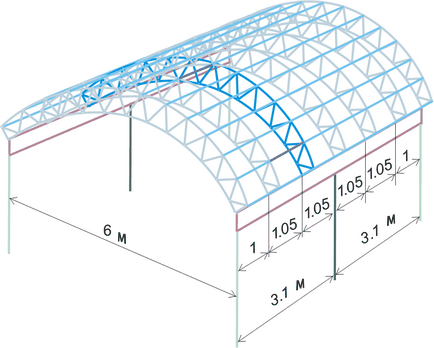
Figura 293.1. Schema generală preliminară a galeriei arcuite.
În general, dacă producția de ferme este planificată dintr-una sau două dimensiuni de profil, calculul unei astfel de ferme rectangulare nu va dura mult timp.
Tensiunile concentrate pentru aceste ferme rectangulare vor fi reacțiile de susținere pentru structurile de arc calculate anterior. Aceste sarcini Q vor fi aplicate nodurilor fermei, după cum se arată în figura 554.1.b). Geometria generală a structurii este prezentată în figura 554.1.a):
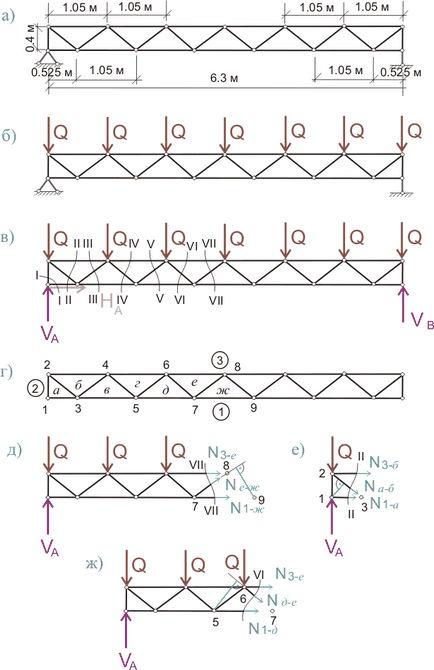
Figura 554.1. Geometria generală și schemele de calcul pentru o structură dreptunghiulară.
Pentru a simplifica calculul, se presupune că lungimile tuturor nivelelor dintre nodurile din centura superioară sunt aceleași.
Determinarea forțelor în barele de ferastraie
Calculul fermelor va fi efectuat prin metoda secțiunilor, ale căror principale prevederi sunt stabilite separat.
Când am calculat fermele arcuite, am aflat că reacțiile de sprijin din aceste ferme pot varia în funcție de opțiunea de încărcare a zăpezii luată în considerare. Pentru calcule ulterioare, luăm în calcul valoarea maximă posibilă a reacțiilor de susținere, atunci încărcătura în fermă din ferme arcuite va fi Q = 796,1 kg.
În plus, ferma va avea o încărcătură distribuită uniform din greutatea proprie a fermei, care, de asemenea, nu ne este cunoscută inițial, ceea ce înseamnă că ferma ar trebui să fie calculată suplimentar pentru această încărcătură. Cu toate acestea, ținând seama de faptul că greutatea proprie a fermei va fi relativ mică, pentru a simplifica calculele, această încărcătură distribuită din greutatea sa proprie poate fi adusă în mod condiționat la concentrat în nodurile fermei. De exemplu, dacă ferma va cântări aproximativ 28 kg, atunci sarcinile suplimentare concentrate vor fi 28/7 = 4 kg, atunci încărcările de proiectare vor fi:
Q = 796,1 + 4 ≈ 800 kg
Deoarece avem o fermă simetrică, la care aceeași încărcătură este aplicată și simetric, atunci reacțiile de referință vor fi egale una cu cealaltă și vor fi:
Valoarea componentei orizontale a reacției lagărului la rulment A va fi zero, deoarece sarcinile orizontale din schema noastră de calcul nu este, deci componenta orizontală a reacției pe un suport A arătat în figura 554.1.v) pal violet.
De asemenea, în figura 554.1.c) sunt secțiunile de-a lungul cărora este posibil să se calculeze forțele în toate tijele structurii, ținând cont de simetria structurii și a sarcinilor. Apoi, vom lua în considerare calculul a doar 4 secțiuni.
Marcajul prezentat în figura 554.1.d) înseamnă că ferma are:
Tijele centurii inferioare: 1-a, 1-in, 1-d, 1-ж;
Tijele curelei superioare: 3-b, 3-d, 3-e;
Deformațiile: a-b, b-in, c-d, g-d, d-e, e-g.
Dacă este necesar, puteți folosi un apostrof pentru a marca tijele simetrice cu cele indicate.
Dacă sarcina este de a calcula toate tijele fermei, atunci este mai bine să faceți o masă în care sunt inserate toate barele fermei. Apoi, rezultatele calculelor, în special valorile tensiunilor de compresiune sau de întindere, vor fi incluse în acest tabel.
În toate secțiunile prezentate în Figura 554.1, forțele N sunt direcționate astfel încât să provoace întinderea în tijele considerate. Dacă, prin rezultatele calculului, forța din tija în cauză este negativă, aceasta înseamnă că forțele normale de compresiune vor acționa asupra acestei tije.
Noi continuăm să considerăm secțiunile transversale.
secțiunea II-II (Figura 554.1.e)
Să compunem ecuația de momente față de nodul 3, aceasta ne va permite să determinăm forța din tija 3-b:
unde l este brațul acțiunii forței Q și reacția de susținere VA. egală cu distanța dintre nodul 1 și nodul 3 orizontal, conform schemei de proiectare acceptate l = 0,525 m; h este brațul acțiunii forței N3-a. egală cu înălțimea fermei, în acest caz h = 0,4m. Aceasta înseamnă că, în realitate, înălțimea totală a structurii, luând în considerare secțiunile curelelor superioare și inferioare, va fi puțin mai mare, deoarece în acest caz înălțimea este distanța dintre axele neutre ale curelelor superioare și inferioare.
Pentru a determina tensiunile în tija a-b, compunem ecuația de momente față de nodul 1:
În acest caz, h 'este brațul aplicării forței Nb-b este înălțimea unui triunghi cu unghi drept. Brațul a fost definit după cum urmează, valoarea unghiului a între tijele 1-a și a-b este calculată mai întâi.
tga = 0,4 / 0,525 = 0,762
unde 0.4 și 0.525 sunt lungimile tijelor - picioarele unui triunghi dreptunghiular.
h '= 0,525sina = 0,525; 0,606 = 0,318 m
Forțele din tija 1-a vor fi egale cu zero, așa cum se poate verifica ușor prin ecuația de momente față de nodul 2:
Să verificăm corectitudinea calculelor, compunând ecuațiile proeminențelor forțelor pe axele principale:
O mică eroare în calculele au trecut peste, datorită faptului că sunt calcule exacte cu o zecimală, și în valorile funcțiilor trigonometrice sunt specificate numai 3-4 zecimale. Dar, în acest caz, nu este necesară o mare precizie. În general, cu astfel de încărcături, o eroare de până la 1 kg poate fi ignorată.
secțiunile VII-VII (figura 554.1.d)
Pentru a determina forțele din tija 1-x, formăm ecuația de momente față de nodul 8:
Pentru a determina forțele din tija, să compunem ecuația de momente față de nodul 7:
N3-e = (800 · 4.725 - 2800 · 2.625) /0.4 = - 8925 kg (lucrează la comprimare)
Pentru a determina forțele din e-tija, compunem ecuația de momente față de nodul 9:
Să verificăm corectitudinea calculelor
Pentru o mai bună reprezentare a tabloului general, permiteți-ne să verificăm încă câteva secțiuni
secțiunea VI-VI (figura 554.1.zh)
Pentru a determina forțele din tija 1-d, compunem ecuația de momente față de nodul 6:
Pentru a determina forțele din tijă, să scriem ecuația de momente față de nodul 5:
Să verificăm corectitudinea calculelor determinând proiecțiile forțelor pe axa x:
secțiunea III-III
Forțele din tija 3-b sunt deja cunoscute de noi, prin urmare, pentru a determina forțele din bare, compunem ecuația de momente față de nodul 5:
Forța din tija 1-in este în mod clar mult mai mică decât în tija 1-x și, prin urmare, în acest caz nu ne interesează, deoarece intenționăm să realizăm cureaua inferioară dintr-o conductă dintr-o secțiune. Și pentru a determina corectitudinea calculelor în acest caz, determinăm proiecțiile forțelor pe axa y:
Acum avem toate datele de baza pentru calculul ulterior
Selectarea unei secțiuni
La prima vedere cel mai încărcat este tija curelei inferioare 1-ж. pe care acționează forța longitudinală de tracțiune N1-x = 9450 kg. Cu toate acestea, solicitările în tijă comprimată 3 ca urmare a îndoirii longitudinale pot fi chiar mai mari, prin urmare, mai întâi de toate, verificăm rezistența acestei bare speciale prin următoarea formulă:
unde φ este coeficientul de îndoire longitudinală, F este aria secțiunii profilului, cm, R este rezistența de proiectare a materialului profilat. În cazul în care rezistența la proiectare nu este cunoscută în prealabil, atunci pentru fiabilitate se recomandă să se ia unul dintre cele minimale R = 2300 kg / cm2.
Calculul barelor comprimate nu diferă de calculul coloanelor. prin urmare, numai etapele principale de calcul sunt prezentate mai jos fără explicații detaliate.
Mai întâi determinați aria secțiunii transversale a profilului. Pentru o tijă întinsă 1-x, această zonă va fi:
F = N / R = 9450/2300 = 4,11 cm2
Prin țevi profilate sortiment rectangulare satisface această secțiune de țeavă cerință 50h30h3 mm, aria secțiunii a unei conducte va fi F = raza 4,21 cm 2 minim de girație i = 1,16 cm. Verificați dacă această conductă pentru coardă superioară comprimată, la fel ca și cureaua de țevi de secțiune transversală diferită - complexitatea suplimentară a tehnologiei, nu justifică numai într-un volum mic de muncă, doar ceva de a face 2 ferma.
Cu o rază de inerție i = 1,14 cm, valoarea coeficientului de flexibilitate va fi
λ = μl / i = 1,05 / 1,16 = 90,5 ≈ 90
apoi, conform tabelului 2, coeficientul de îndoire este φ = 0,629 (determinat prin interpolarea valorilor 2050 și 2450)
8925 / (0,629 · 4,21) = 3368 kgf / cm2 >> R = 2300 kgf / cm2;
După cum vedem, această valoare a stresului este mult mai mult decât permisă. Dacă se utilizează o țeavă de 50x40x3 mm cu o secțiune transversală de 4,81 cm și o rază de inerție minimă de i = 1,54 cm pentru realizarea curelelor, rezultatul calculelor va fi următorul:
λ = 1,05 / 1,54 = 68,2 ≈ 68
8925 / (0,77-4,81) = 2409 kgf / cm2> R = 2300 kgf / cm2;
După cum vedem și o astfel de conductă pentru a ne asigura că nu este suficientă forța. Ei bine, atunci pot exista diferite opțiuni care pot fi utilizate pentru a face 50h40h3.5 curele țeavă mm, cu o suprafață de 5,49 cm2 secțiune transversală, care oferă în mod clar marja de siguranță dorită, este posibil să se ia în considerare alte opțiuni, dar ne vom concentra pe ea.
Acum trebuie să verificați flexibilitatea maximă admisibilă a benzii întinse de la planul friptului. Potrivit SNP II-23-81 * „Structura de oțel“, această flexibilitate pentru membrii fermelor de tensiune nu trebuie să depășească 400. Prin urmare, la fabricarea tubului trebuie să fie plasate astfel încât 50 - aceasta era lățimea conductei, dar nu și înălțimea, în timp ce cu o rază de i = 1,81 cm flexibilitatea curelei inferioare va fi:
λ = 1,630 / 1,81 = 348
Am observat această cerință, putem proceda la calcularea brațelor și coloanelor. Cea mai încărcată brățară va fi tija comprimată a bmw. Lungimea estimată va fi:
l = 0,525 / cos37,3 ° = 0,525 / 0,7954 = 0,66 m sau 66 cm
Pentru o forță învecinată, pentru o anumită rezistență de proiectare, pentru a asigura rezistență, o conductă de cel puțin
F = N / R = 3300,4 / 2300 = 1,43 cm2
Pentru o bretea comprimată cu o posibilitate de îndoire longitudinală, secțiunea transversală trebuie să fie mai mare, atât cât nu este cunoscută, dar suntem acum oameni de știință și, prin urmare, vom lua imediat conducta cu o marjă bună pentru zona secțiunii transversale.
Mai întâi, să verificăm tubul pătrat de 25x25x2,5 mm, având o secțiune transversală de 2,14 cm 2. Raza inerției este i = (1,77 / 2,14) 1/2 = 0,91 cm Apoi:
3300,4 / (0,74; 2,14) = 2084 kgf / cm2 Această țeavă îndeplinește cerințele și chiar și cu o anumită marjă. Rămâne să aflăm care va fi aproximativ masa totală a fermei: m = 1,41 (0,66; 12 + 0,4; 2) + 4,31; 6,3; 2 = 66,6 kg Aceasta este de 2 ori mai mare decât am presupus la început, dar, în general, creșterea totală a încărcăturii, ținând cont de greutatea proprie a fermei, va fi foarte mică, aproximativ 0,6%. Cu toate acestea, căutarea variantei optime poate fi continuată, în acest articol vom vorbi despre ceea ce este. Sunt îndeplinite toate condițiile necesare pentru rezistență și stabilitate, dar nimeni nu interzice utilizarea profilurilor cu o secțiune transversală mai mare pentru fabricarea fermelor. Rămâne să se calculeze lungimile și picioarele sudurilor, dar acesta este un subiect separat.