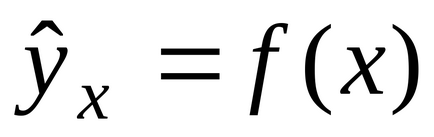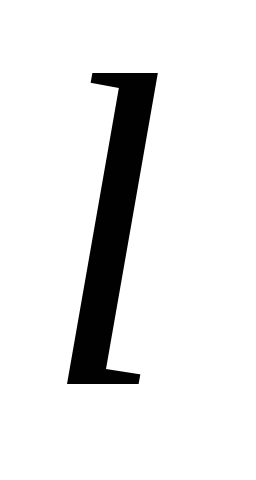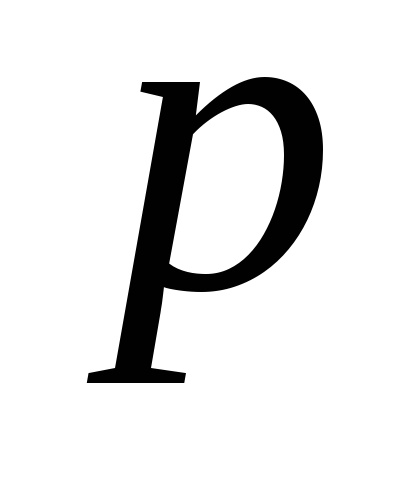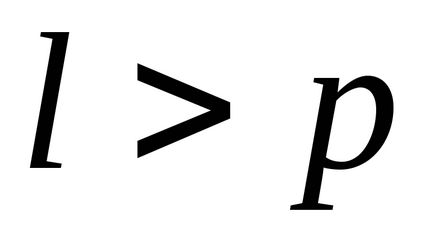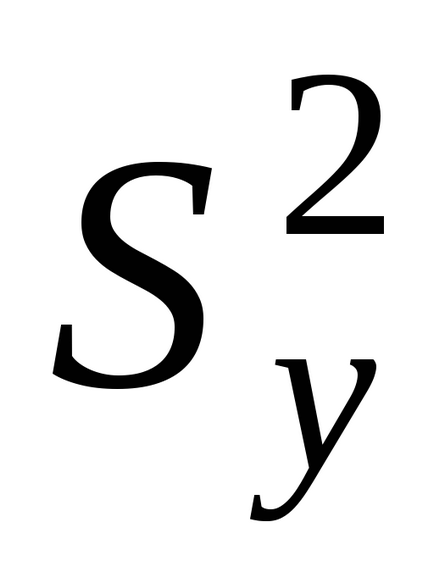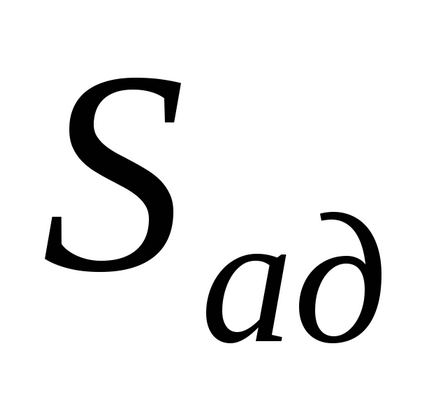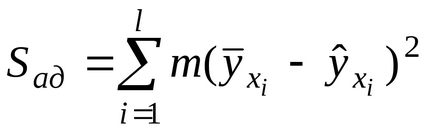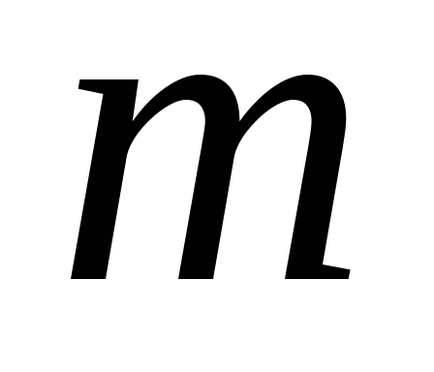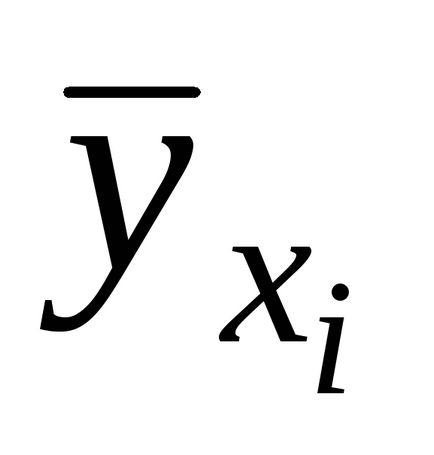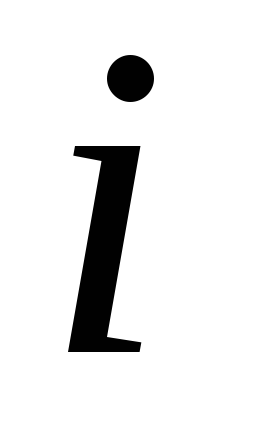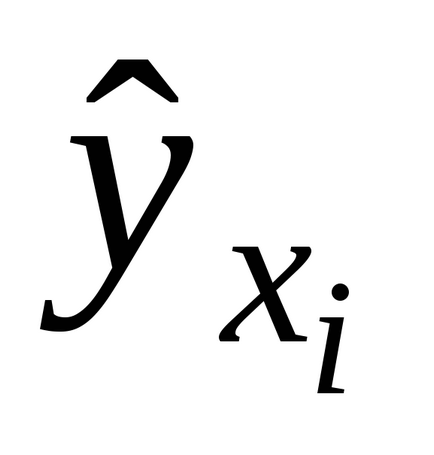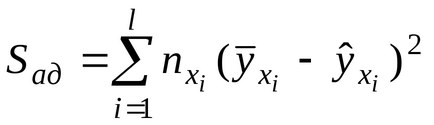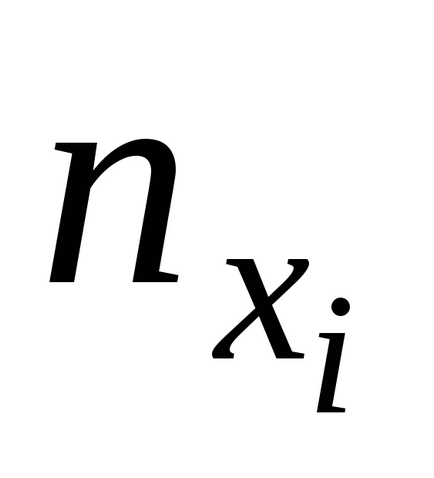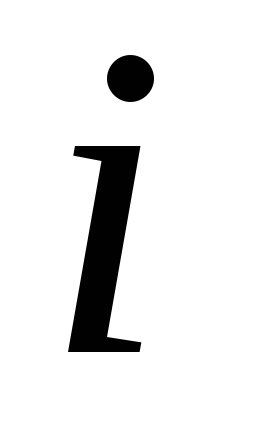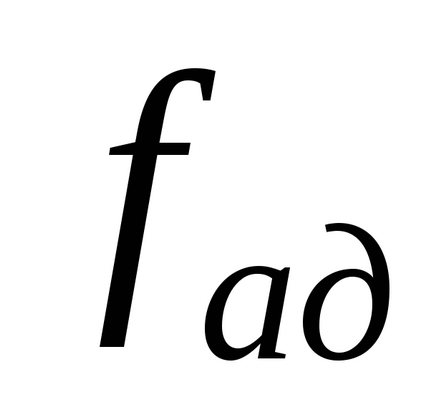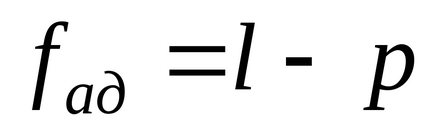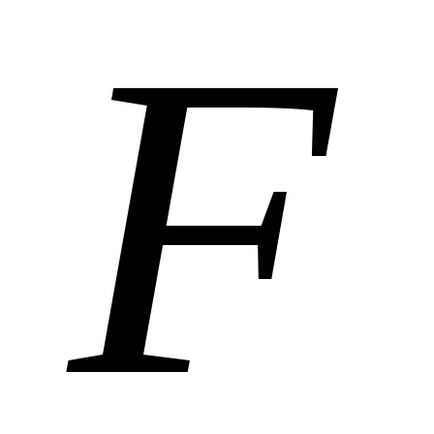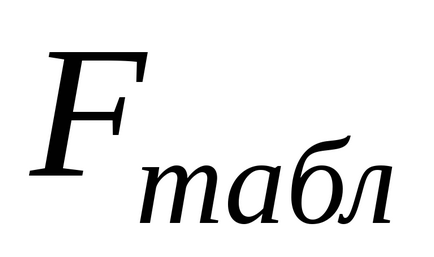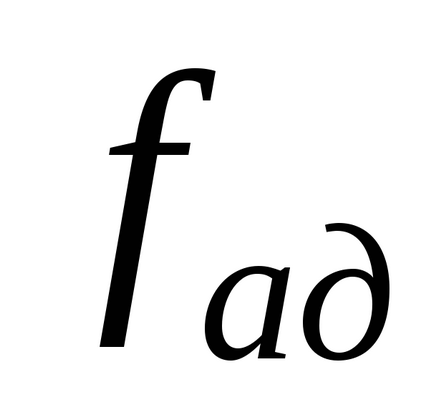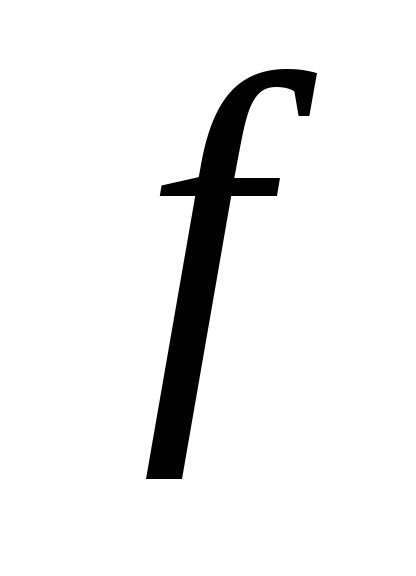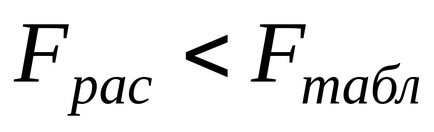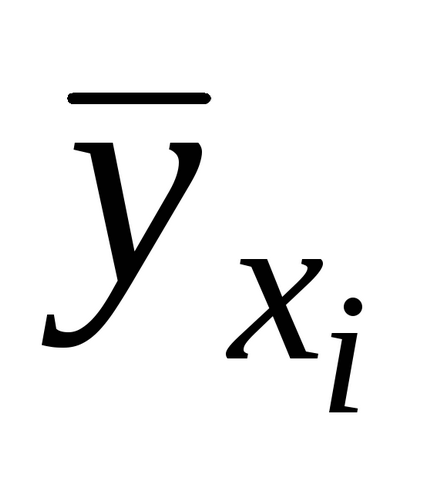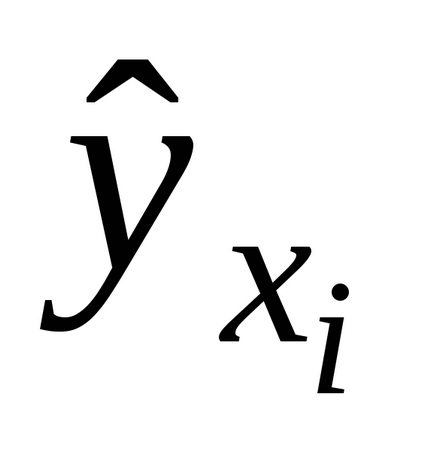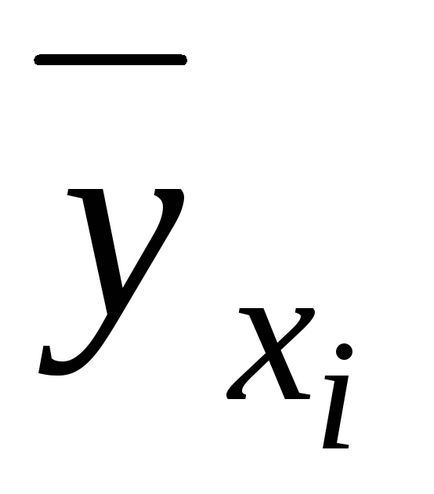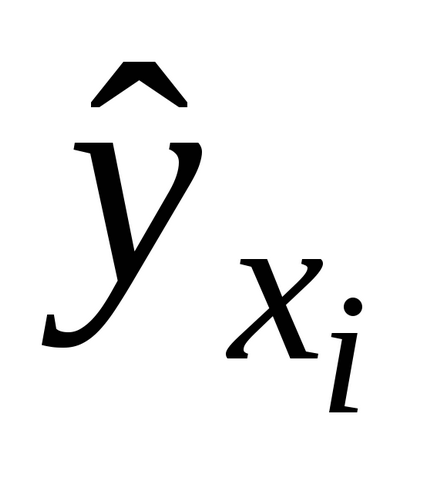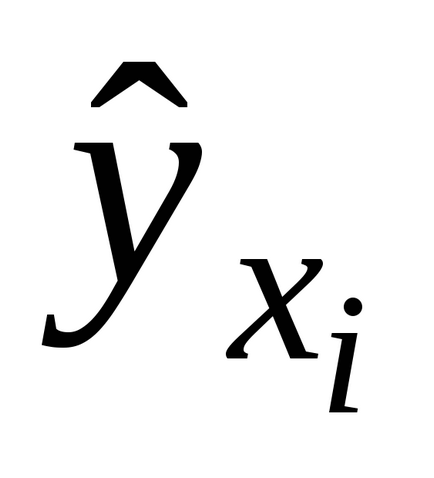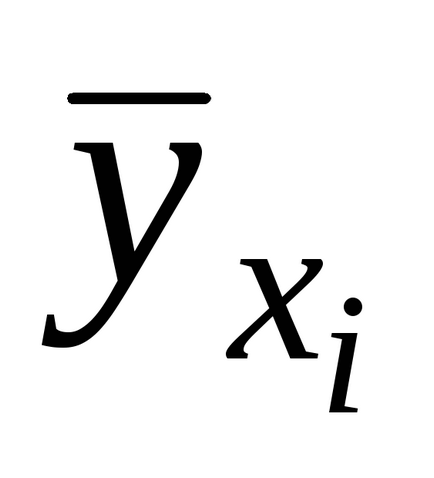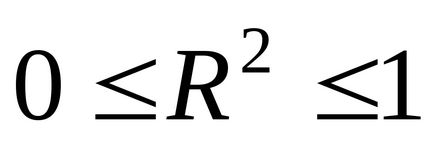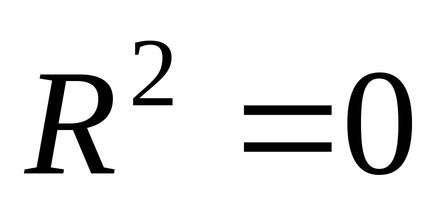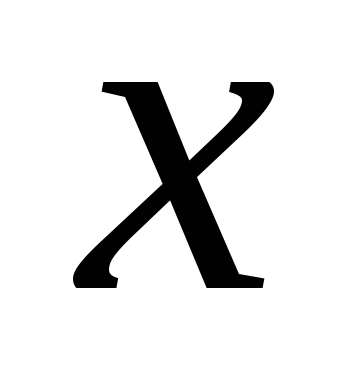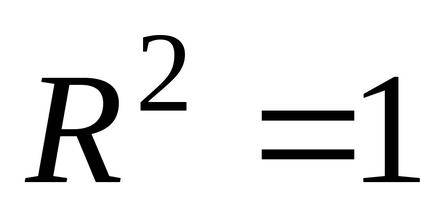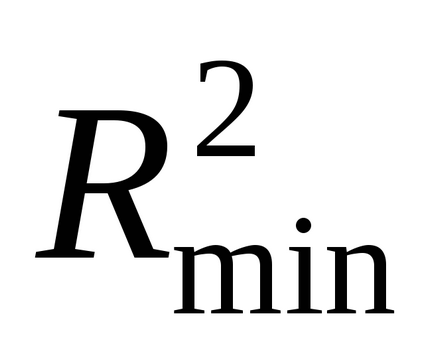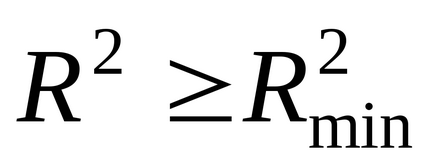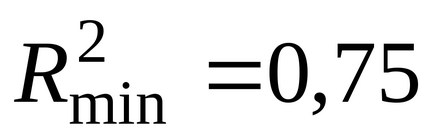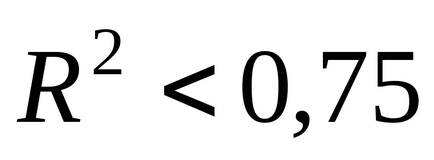Modelul de regresie
, Pe baza rezultatelor experimentului, este posibil să se calculeze valorile răspunsului în diferite puncte din gama de factori.
Verificarea adecvării modelului matematic face posibil ca experimentatorul să răspundă la întrebarea dacă modelul construit va prezice valorile cantității de ieșire cu aceeași precizie ca și rezultatele experimentale.
lăsa
- numărul de experimente din planul experimental sau numărul de serii de experimente paralele, dacă experimentele sunt duplicate,- numărul de coeficienți estimați de regresie a modelului matematic.
Testul de adecvare este posibil numai cu
, și anume dacă designul experimental este nesaturat.
Pentru a verifica adecvarea modelului, este necesar să se cunoască varianța varianței de reproductibilitate
, care poate fi calculată, în funcție de tehnica de duplicare a experienței (a se vedea 1.11).
1.13. Procedură pentru verificarea caracterului adecvat al modelului
1. Determinați suma pătratelor care caracterizează caracterul adecvat al modelului
. Cu o duplicare uniformă a experimentelor
,
unde
- numărul de experimente duplicate din fiecare serie;- valoarea medie a rezultatelor în-acea serie de rezultate duplicate,- valoarea teoretică, calculată cu ajutorul modelului de regresie obținut.
În caz de duplicare inegală
,
- Numărul de experimente duplicate din -acea serie.
2. Calculați numărul de grade de libertate
varianța de adecvare. Cu orice metodă de duplicare.
3. Calculați varianța de adecvare
Cu ajutorul lui
-Testul Fisher verifică omogenitatea varianței de adecvare (18) și variația reproductibilității (19). Procedând astfel, calculați
care este comparat cu valoarea tabelului
, găsită la nivelul de semnificație aleasă α pentru numărul de grade de libertate , în numărător șiîn numitor ().
În cazul în care
, atunci modelul este considerat adecvat și poate fi folosit pentru a descrie obiectul. În caz contrar, modelul nu este adecvat.
Metoda considerată de verificare a gradului de adecvare joacă un simț fizic simplu.
Această procedură se bazează pe testarea ipotezei de omogenitate a dispersiei de adecvare și varianță, care caracterizează eroarea experimentului. Rețineți că varianța de adecvare caracterizează discrepanța dintre rezultatele experimentale
și valorile cantității de ieșire, calculată din ecuația de regresie. Evident, modelul descrie în mod satisfăcător obiectul cercetării, adică este adecvat dacă această discrepanță este cauzată doar de erori experimentale și nu este legată, de exemplu, de o alegere nereușită a tipului de model matematic.
Testarea ipotezei de omogenitate a diferențelor examinate și clarificarea originii comune a erorilor experimentale și discrepanța dintre
și.
1.14. Coeficient de determinare
Ca măsură a modului în care regresia descrie acest sistem de observații, coeficientul de determinare servește.
Coeficientul de determinare caracterizează integral proprietățile de precizie ale ecuației de regresie. Aceasta arată cât de mult din împrăștierea totală a valorilor experimentale relative la media sa se datorează dependenței de regresie:
unde
- valoarea teoretică a caracteristicii efective, calculată cu ajutorul modelului de regresie obținut,- valoare medie,- grupul mediu, adică valorile reale ale rezultatului.
.
În cazul în care
, apoi variațiaeste determinată complet de perturbații aleatorii și de influența factoruluinu a fost găsit.
În cazul în care
, Curba de regresie trece prin toate punctele experimentale. Puteți specifica o limită inferioară a coeficientului de determinare, ceea ce înseamnă că numai în cazul în careEcuația de regresie are un interes practic suficient:. În cazul în care, atunci este puțin probabil ca modelul de regresie să funcționeze.