PATRU DIN NUMERELE PATRU-SEMNIFICATIVE
Ca o abilitate pregătitoare pentru dezvoltarea abilității de a păstra numere de patru cifre, trebuie să stăpâniți soluția de probleme pentru multiplicarea tipului "4 pe 1". Împărțim această sarcină în două subtascuri de tipul "2 de la 1", după cum se arată mai jos.
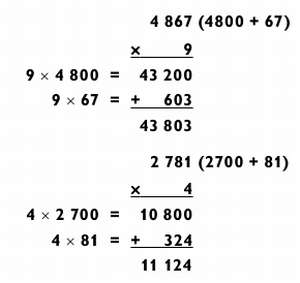
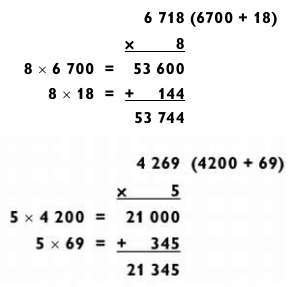
Mastering abilitatea de a multiplica "4 cu 1" va însemna că sunteți gata să pătrat numere de patru cifre. Lăsați exemplul 4267. Folosind aceeași metodă ca și în disputându numerelor cu două și trei cifre, se va face acest lucru cu numărul 4267, rotunjirea-l într-o parte inferioară 267-4000 și cel mai mult - de la 267-4534 x 4534. Multiplicarea 4000 (sarcina "4 pe 1") și apoi adăugați pătratul numărului la care ați schimbat originalul (267 2), după cum se arată mai jos.
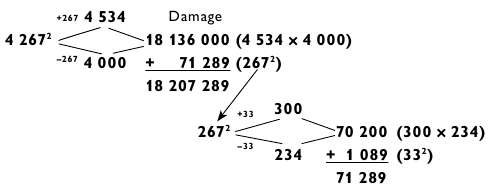
Este deja evident cât de multe acțiuni au loc în acest exemplu. Îmi dau seama că este un lucru de spus: "Adăugați un pătrat 267", și altul - faceți acest lucru și amintiți-vă numărul care ar trebui adăugat. Prin urmare, de îndată ce 4534 x 4 multiplica și de a obține 18,136, puteți spune prima parte a răspunsului cu voce tare: „Optsprezece milioane ...“. Puteți spune acest lucru deoarece numărul original este întotdeauna rotunjit la cea mai apropiată mie. Prin urmare, cel mai mare număr de trei cifre, care va Cuadratura pasul următor va fi 500. Piața 500 este de 250 000. Deoarece restul răspunsului dumneavoastră (în acest caz, 136000) mai mică de 750 000, acest lucru înseamnă că numărul de milioane nu schimba.
După ce pronunțați cuvântul „cele optsprezece milioane ...“, trebuie să se stabilească în memorie numărul de 136 000, înainte de a Cuadratura 267. Asta în cazul în care tehnicile mnemonice din capitolele anterioare vin la salvare! Datorită codului fonetic, numărul 136 poate fi transformat în deteriorarea cuvântului (1 = d .3 = m. 6 = j) [14]. Acum, îndrăzniți să treceți la următoarea parte a problemei, amintiți-vă doar de daunele (și existența a trei zerouri suplimentare la sfârșitul numărului). Dacă la un moment dat, în mijlocul de calcul uitați problema originală, puteți lua fie o scurtă privire la numărul inițial, sau, în cazul în care nu sunt scrise, cere publicul să repete sarcina (în scopul de a crea iluzia că sunt din nou încep să abordeze, în timp ce sunt au făcut unele calcule)!
Ca rezultat al tăierii unui număr de trei cifre (studiat anterior), vei primi 71.289. Mi-a fost dificil să-mi amintesc sute de răspunsuri (în acest caz 2).
M-am confruntat cu aceasta, recurgând la ajutorul degetelor (aici - două degete). Dacă uitați ultimele două cifre (89), puteți reveni la numărul inițial (4267), puteți seta ultimele două cifre pătrat (67 2 = 4489) și luați ultimele două cifre ale numărului.
Pentru a calcula răspunsul final, trebuie să adăugați 71 289 daunelor (adică 136 000), iar suma lor 207 289 poate fi deja rostită cu voce tare.
Este dificil să se ia primul loc în ceea ce privește numărul de probleme de formare cu Helen Keller [15]. dar sclavul negru Thomas Fuller, născut în Africa în 1710, vine literalmente pe tocuri. El nu a fost doar analfabet, dar nu a studiat nici o zi în viața lui. Fiind "proprietatea" lui Elizabeth Cox, Thomas Fuller a lucrat în câmpurile din Virginia. El a stăpânit duce la 100, iar apoi a dezvoltat ei „abilități de calcul“ prin numărarea obiectelor care sunt întotdeauna la îndemână, cum ar fi banițe de boabe de grâu, semințe de in și numărul de fire de păr în coadă de vacă (2872 threadline).
Plecând de la un simplu cont, Fuller a învățat cum să calculeze cât de mult șindrilă este necesar pentru a acoperi acoperișul casei; câți poli vor fi necesari pentru garduri și lucruri similare. Abilitățile sale uimitoare s-au dezvoltat și, împreună cu ele, a crescut reputația lui. Deja la o vârstă înaintată, el a acceptat provocarea a două Pennsylvanians, fiind de acord să-și demonstreze abilitățile în calculul numerelor în minte și care ar putea cauza dificultăți pentru cei mai buni calculatoare de viteză. De exemplu, ei au întrebat: "Să presupunem că un fermier are șase scroafe, fiecare dintre ele va avea șase femele în primul an și toate se vor înmulți în aceeași progresie timp de opt ani; câte scroafe va avea agricultorul în cele din urmă? "Sarcina poate fi scrisă ca 7
8 x 6, adică 7 x 7 x 7 x 7 x 7 x 7 x 7 x 7 x 6. În mod literal după zece minute, Fuller a răspuns: 34 588 806.
După moartea sa, în 1790, ziarul columbian Centinel a raportat că „Fuller ar putea calcula numărul de șantiere, picioare, inci și o treime dintr-un inch [16] pentru orice distanță dată, numit diametrul orbitei Pământului, iar rezultatele fiecărui calcul a dat răspunsul corect în mai puțin timp, decât nouăzeci și nouă de oameni din o sută ar face-o pe hârtie ". Când a fost întrebat Fuller dacă îi pare rău că nu a primit o educație tradițională, el a răspuns: "Nu. Cel mai bun lucru pe care îl am este lipsa educației: printre mulți oameni învățați sunt mari nebuni ".
Să lăsăm un număr mai mare de patru cifre: 8431 2.
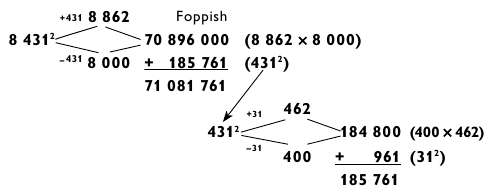
Nu voi re-descrie toate acțiunile, ca în ultima sarcină, vă voi atrage atenția doar asupra anumitor puncte. După efectuarea pasului 8 x 8862 = 70 896, este clar că mai mult de 896 750, astfel încât unitatea poate transfera la MSB. Într-adevăr, ca mai mult de 400 431 2 2 = 160 000, cu siguranta nevoie de o unitate de transfer în adăugarea de 431-2 896 000. Prin urmare, în această etapă, puteți spune cu siguranță cu voce tare: „Șaptezeci un milion de ...“
Când se cristalizează 431, ajungem la 185.761. Adăugăm 185 și 896, lăsăm 1081, iar noi spunem restul răspunsului.
Dar amintiți-vă, am anticipat deja transferul unei unități, deci spuneți: "... 81 mii ... 761". Munca se face!
Pentru un punct mai subtil al calculelor, vom arăta exemplul 2753 2.
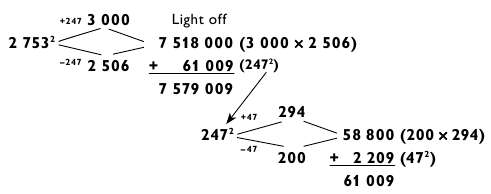
Puteți, desigur, scădea 2753 - 247 = 2506, dar acest lucru este mai dificil.
Apoi lucrăm în modul obișnuit, înmulțind 3000 x 2506 = 7 518 000; transformăm 518 în cuvinte luminoase [17] și spunem cu voce tare prima parte a răspunsului: "Șapte milioane ...". Aici se poate argumenta, deoarece 518 este mai puțin de 750, deci nu va exista o unitate de transport.
Apoi adăugăm pătratul numărului 247. Nu uitați că 247 poate fi obținut rapid ca o adăugare pentru 753. Apoi treceți la răspunsul final, așa cum sa făcut în exemplul anterior.
EXERCIȚIU: SQUARES DE NUMERI PATRU SEMNIFICAȚI