Definiție Un asimptot pentru o curbă este o linie dreaptă a cărei distanță față de un punct de pe curbă tinde să atingă zero, deoarece distanța de la originea acestui punct de-a lungul curbei este nelimitată; .
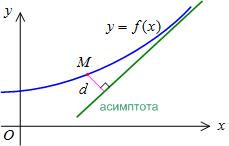
Asimptotele pot fi verticale, orizontale și înclinate.
O linie dreaptă este o asimptotă verticală. dacă
Pentru a găsi asimptotele verticale, este necesar să găsiți aceste valori. sub care funcția crește sau scade fără limită. De obicei, acestea sunt puncte de discontinuitate a celui de-al doilea tip.
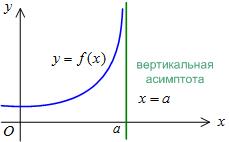
Exemplul 1. Găsiți asimptotele verticale ale graficului funcției.
Soluția. Numitorul dispare în puncte. Deoarece și. în consecință, liniile sunt asimptote verticale.
O linie dreaptă este o asimptote orizontală. în cazul în care.
Pentru a găsi asimptota orizontală, trebuie să găsim limita funcției pentru u.
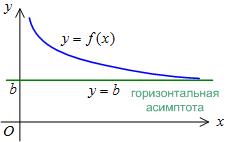
Exemplul 2. Găsiți asimptota orizontală a graficului funcției.
Soluția. Noi găsim limita. În consecință, asimptota orizontală (în partea stângă) a graficului funcției date este o linie dreaptă. Rețineți că. astfel încât nu există asimptote orizontale la dreapta.
Ecuația asimptotei oblice este sub forma,
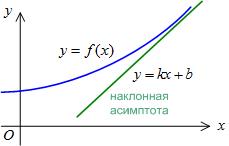
Exemplul 3. Găsiți asimptota oblică a graficului funcției.
Soluția. Găsiți panta asimptotei :.
Mai mult, se calculează termenul liber al ecuației asimptote:
Astfel, asimptota pantei graficului acestei funcții este o linie dreaptă.
Întrebarea. Asimptotul orizontal al graficului unei funcții este linia