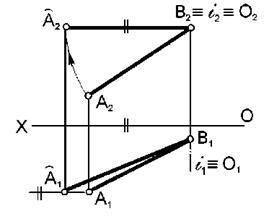
Prin transformarea proiecțiilor pot fi rezolvate următoarele probleme:
1. Determinarea valorii naturale a unui segment de linie dreaptă și a unghiurilor de înclinare a acesteia către planurile proeminențelor.
2. Determinarea distanței de la un punct la o linie dreaptă.
3. Determinarea distanței dintre liniile paralele.
4. Determinarea distanței dintre liniile drepte încrucișate.
5. Determinarea dimensiunii unghiului dihedral.
6. Determinarea distantei de la un punct la un plan.
7. Determinarea distanței dintre planurile paralele.
8. Determinarea valorii reale a unei figuri plane.
9. Determinarea unghiului de înclinare a unei linii drepte și a unui plan.
10. Determinarea unghiurilor de înclinare a planului în planurile de proiecții etc.
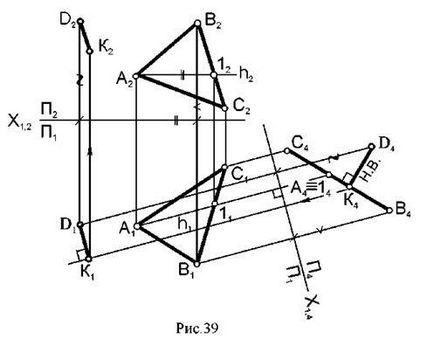
Determinați distanța de la punctul D la planul ABC (Figura 39). Pentru a determina AVS distanța dorită transformă avionul la proiectat să-l țină în această orizontală (h) și o nouă aprovizionare perpendicular pe planul P4 h și deci H1,4 perpendicular proiecție orizontală (h1), astfel planul ABC ar fi perpendicular pe planul P4 CÆUTAREA distanta - (D4 K4) este valoarea perpendicularului scazut de la. D4 pe linia A4 B4 C4 (proiecția planului ABC pe planul P4).
Întrebări pentru auto-examinare.
1. Care sunt modalitățile de a converti proiecțiile?
2. Care este esența imaginii de proiecție în calea schimbării planurilor de proiecție?
3. Listați cele 4 probleme principale rezolvate prin metoda înlocuirii planurilor de proiecții.
4. Ce tipuri de probleme pot fi rezolvate prin schimbarea planurilor de proiecție?
Curs 6. Metodă de rotație.
Metoda conform invenției constă în schimbarea poziției de rotație a obiectului specificat pe diagrama, astfel încât unele dintre elementele sale luate în ceea ce privește o anumită poziție a planurilor de proiecție și proiectate fără distorsiuni.
Începeți transformarea în acest fel, trebuie să pregătiți dispozitivul de rotație: axa, centrul și raza de rotație.
Poziția axei de rotație distinge mai multe tipuri ale acestei metode.
Rotirea pe o axă perpendiculară pe planul proeminențelor. Când se rotește un punct în spațiu în jurul unei axe perpendiculare pe planul orizontal de proiecție, punctele de proiecție sunt deplasate după cum urmează: orizontală - circumferențial, front - într-o linie dreaptă paralelă cu axa de coordonate (sau perpendicular pe axa de rotație) (Tabel 40).
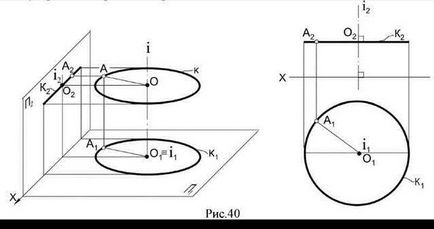
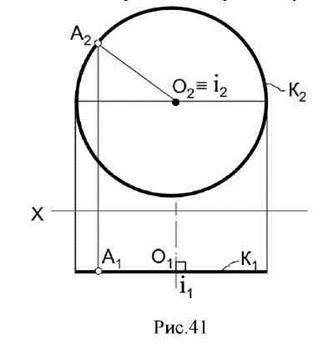
Dacă axa de rotație este perpendiculară pe planul frontal al proeminențelor, diagrama obținută la modelul invers (Fig.41).
Pentru a roti o linie dreaptă în jurul axei, este suficient să rotiți punctele sale în același unghi. Când rotiți planul, trebuie să rotiți elementele definitorii: trei puncte, o linie dreaptă și un punct și așa mai departe. Această metodă este convenabilă pentru a determina dimensiunea reală a unui segment de linie și unghiul său față de planul de proiecție, axa de rotație a efectua în mod eficient printr-unul dintre punctele de o linie dreaptă, pentru a evita construcții inutile.
Determina valoarea naturală a segmentului de linie AB (Figura 42)
Pentru a direcționa în mărime naturală proiectată, acesta trebuie să fie poziționat în paralel cu un - un plan de proiecție, ceea ce înseamnă că unul dintre proiecția sa trebuie să fie paralelă cu axa proiecției: