Caracteristicile de performanță ale unui motor asincron sunt reprezentate grafic în funcție de viteza de rotație n2, eficiență # 951; cuplul util (cuplul pe ax) M2, factorul de putere cos # 966; și curentul stator I1 de la puterea utilă P2 la U1 = const f1 = const.
Caracteristica de viteză este n2 = f (P2). Viteza rotorului motorului de inducție este n2 = n1 (1 - s).
Alunecarea s = PE2 / Pem, t. E. Alunecarea motorului asincron, și deci viteza este determinată de raportul dintre pierderile electrice în rotor la puterea electromagnetică. Neglijând pierderile electrice în rotor în modul inactiv, putem lua P2 = 0, deci s ≈ 0 și n20 ≈ n1.
Pe măsură ce sarcina pe arborele motorului asincron crește, raportul s = Pе2 / Pem crește, ajungând la 0,01-0,08 la sarcina nominală. În concordanță cu aceasta, dependența n2 = f (P2) este o curbă ușor înclinată față de axa abscisă. Cu toate acestea, pe măsură ce rezistența rotorului activă a motorului r2 crește, unghiul de înclinare al acestei curbe crește. În acest caz, modificările frecvenței motorului asincron n2 cu fluctuații ale sarcinii P2 cresc. Acest lucru se explică prin faptul că, cu creșterea r2 ', pierderile electrice în rotor cresc.
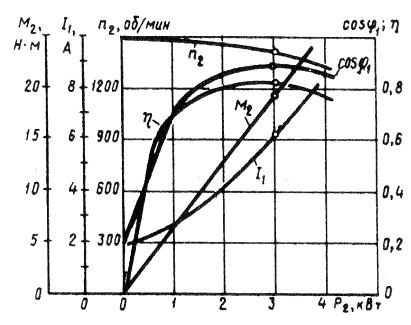
Fig. 1. Caracteristicile de performanță ale unui motor de inducție
Dependența lui M2 = f (P2). Dependența momentului util pe arborele motorului asincron M2 la puterea utilă P2 este determinată de expresia M2 = P2 / 2 = 60 P2 / (2nn2) = 9,55P2 / n2,
unde P2 este puterea netă, W; # 969; 2 = 2πf 2/60 - viteza de rotație unghiulară a rotorului.
Din această expresie rezultă că dacă n2 = const, atunci graficul lui M2 = f2 (P2) este o linie dreaptă. Dar, motor asincron cu creșterea P2 sarcină a vitezei rotorului scade și, prin urmare, arborele de util cuplul M2 cu creșterea sarcinii nu crește de încărcare mult mai rapid și, prin urmare, un grafic M2 = f (P2) are o formă curbată.
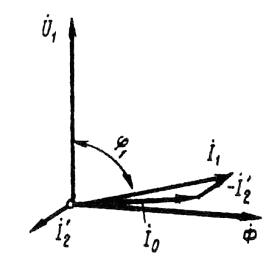
Fig. 2. Diagrama vectorială a unui motor asincron la sarcină scăzută
Cosul 1 = f (P2). Datorită faptului că I1 motor cu inducție stator curent are o componentă reactivă (inductiv) necesare pentru crearea unui câmp magnetic în stator, factorul de putere a motorului de inducție este mai mică decât unitatea. Valoarea cea mai mică a factorului de putere corespunde funcționării la ralanti. Acest lucru se explică prin faptul că curentul fără sarcină al motorului I0 rămâne practic neschimbat sub orice sarcină. Prin urmare, pentru sarcinile mici ale motorului, curentul statoric este mic și într-o mare măsură este reactiv (I1 ≈ I0). Ca urmare, deplasarea de fază a curentului stator în raport cu tensiunea este semnificativă (# 966; 1 ≈ # 966; 0), doar puțin mai mică de 90 ° (figura 2).
Factorul de putere al motoarelor asincrone în modul inactiv nu depășește de obicei 0,2. Prin creșterea sarcinii pe arborele motorului crește componenta activă a curentului I1 și crește factorul de putere, atingând o valoare maximă (0.80-.90) la o sarcină aproape la valoarea nominală. Creșterea suplimentară a sarcinii pe arborele motorului este însoțită de o scădere a cosului 1 care se explică prin creșterea rezistenței inductive a rotorului (x2s) datorită creșterii alunecării și, prin urmare, a frecvenței curentului în rotor.
Pentru a crește factorul de putere al motoarelor asincrone, este extrem de important ca motorul să funcționeze întotdeauna sau cel puțin o parte considerabilă a timpului cu o sarcină apropiată de sarcina nominală. Acest lucru poate fi asigurat numai cu alegerea corectă a puterii motorului. În cazul în care motorul funcționează o parte semnificativă a timpului subîncărcat, apoi pentru a crește cos # 1, este de dorit să se reducă tensiunea U1 la motor. De exemplu, în motoarele care funcționează la conectarea înfășurării statorului triunghi, se poate face pentru reconectarea înfășurarea statorului într-o stea, provocând o scădere a tensiunii de fază în timp. În acest caz, fluxul magnetic al statorului și, în consecință, și curentul de magnetizare, scade aproximativ în timp. În plus, componenta activă a curentului stator crește oarecum. Toate acestea contribuie la creșterea factorului de putere al motorului.
În Fig. 3 sunt grafice ale dependenței cos # 1; motorul de inducție din sarcină la conectarea înfășurărilor statorului cu o stea (curba 1) și un triunghi (curba 2).
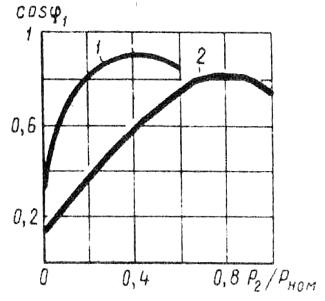
Fig. 3. Dependența cos # 1, de la sarcină la conectarea înfășurării statorului a motorului cu steaua (1) și triunghiul (2)
