Este foarte simplu! Dacă te uiți la masă, poți vedea că valoarea șirului sinusoidală este foarte asemănătoare cu linia de valori cosinus, numai valorile sunt în ordine inversă. Același lucru vom vedea dacă privim liniile de valori ale tangentei și ale cotangentei. Acum, uită-te la cealaltă masă. Nu este nimic de amintit deloc. Câte grade nu este suficient pentru 180, sinus / cosinus / tangent / cotangent al acestui număr de grade de la primul tabel este egal cu această valoare. Voi explica prin exemplu: 180-150 = 30. Sinusul lui 30 este de 1/2. Sinusul de 150 este, de asemenea, egal cu 1/2. Singurul lucru de retinut din tabelul al doilea este ca valorile sinusoidale sunt pozitive, iar cosinusul, tangenta si cotangenta sunt negative.
Mult noroc în studiu. -)
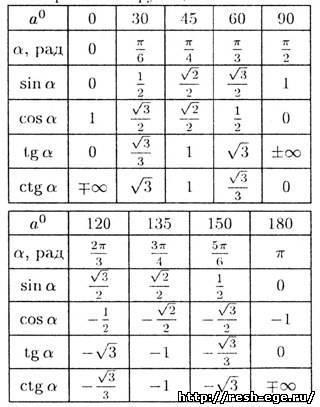
Dacă înțelegeți unghiurile cele mai populare de 0 °, 30 °, 45 °, 60 ° și 90 °, amintirea este destul de simplă.
De exemplu, sinele acestor 5 unghiuri au aceeași ordine de mărime
√0 / 2, √1 / 2, √2 / 2, √3 / 2, √4 / 2 (1)
Adică, numitorul este 2, iar numărătorul este luată rădăcina pătrată a numerelor 0, 1, 2, 3 și 4. Ca urmare, avem
sin0 = 0, sin30 = 1/2, sin45 = √2 / 2, sin60 = √3 / 2 și sin90 = 1.
Pentru cosinusului au aceeași secvență (1), dar colțurile trebuie să fie luate în ordine inversă față de 90 °, 60 °, 45 °, 30 ° și 0 °. Apoi, obținem
cos90 = 0, cos60 = 1/2, cos45 = √2 / 2, cos30 = √3 / 2 și cos0 = 1.
În ceea ce privește tangenta și cotangenta, ele pot fi pur și simplu calculate din formule
tgα = sinα / cosα și ctgα = cosα / sinα.
De exemplu, pentru tangentele unghiurilor 0 °, 30 °, 45 °, 60 ° și 90 °, avem succesiv
tg0 = 0, tg30 = 1 / √3 tg45 = 1, tg60 = √3 și tg90 = ∞.