3. Găsiți setul de valori ale funcției:

8. Specificați funcția al cărei grafic este prezentat în figură. Linia dreaptă este dată de o ecuație cu forma: y = kx + b, unde b este ordonata punctului de intersecție al liniei drepte cu axa Oy, deci b = -3. Ecuația are forma: y = kx-3. Pentru a găsi panta k - înlocuim coordonatele punctului de grafic (-3; 0) în ecuația ultimă. Obținem: 0 = k + (-3) -3, deci 3k = -3, k = -1. Ecuația necesară este y = -x-3.
12. Găsiți produsul rădăcinilor ecuației:

15. Linia y = x-2 este tangentă la graficul funcției y = f (x) la punctul x0 = -1. Găsiți f (-1).
Punctul de tangență aparține atât tangentei y = x-2, cât și graficului funcției y = f (x). Abscisa punctului de tangență este -1, iar ordonata este găsită prin înlocuirea valorii x = -1 în ecuația tangentă.
y = -1-2 și obținem y = -3.
16. Gasiti unghiul dintre tangenta si graficul functiei y = sin2x + cos2x in punctul (0; 0) si axa Ox.
Semnificația geometrică a derivatului este că derivatul numeric al funcției la punctul xo
este egală cu tangenta unghiului de înclinare a tangentei la graficul funcției în punctul cu abscisa xo. Prin urmare, scriem egalitatea:
tgα = f '(xo). Să găsim derivatul funcției date: y '= 2cos2x-2sin2x.
f '(xo) = 2cos0-2sin0 = 2. Prin urmare, tgα = 2, prin urmare α = arctg2.
17. Gasiti zona unui triunghi isoscel, daca partile laterale ale acestuia sunt 16 cm, 17 cm, 17 cm. Concluzionam ca baza unui triunghi isoscel este partea egala cu 16 cm.
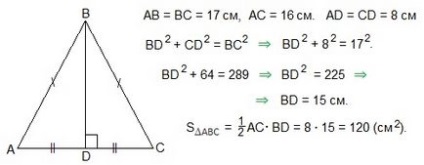
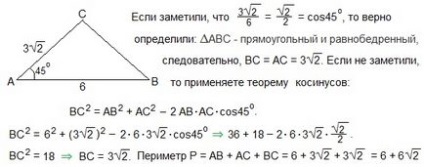
18. Găsiți perimetrul triunghiului dacă cele două părți ale acestuia sunt 6 și 3 ale rădăcinii celor două, iar unghiul dintre ele este de 45 °.

25. Cutia conține 4 creioane colorate și 10 creioane simple. Care este cel mai mic număr de creioane care trebuie luate, astfel încât să fie cel puțin trei dintre aceștia?
Din moment ce putem lua 4 creioane la rând și toate pot deveni colorate, atunci trebuie să luăm încă 3 creioane, care, sigur, se vor dovedi a fi simple. Prin urmare, tot ce trebuie să faceți este să luați 7 creioane, astfel încât să fie cel puțin trei creioane simple între ele.
Formare de succes pentru tine, prieteni!